In this case, we apply the topology optimization (TO) method to the design of a two-dimensional Y‑branch splitter. By directly optimizing the material distribution within the design region and allowing the algorithm to explore freely throughout the design space, we demonstrate the powerful capability of topology‑based inverse design in both structural generation and performance optimization of photonic devices.
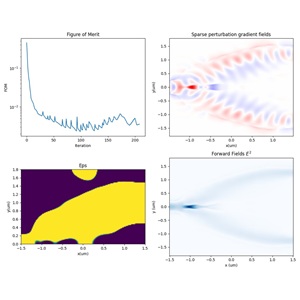
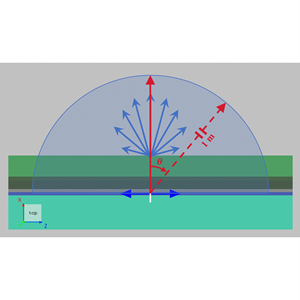
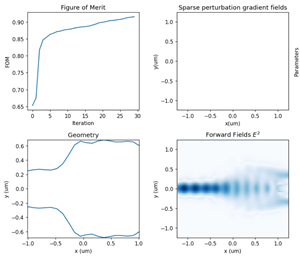
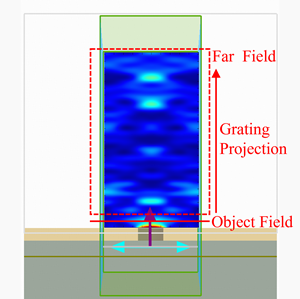
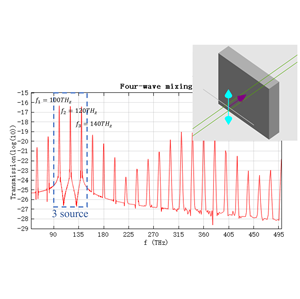
Organic light-emitting diode (OLED) devices are widely used in high-end displays and solid-state lighting due to their self-emissive nature, wide viewing angle, high contrast ratio, and compatibility with flexible form factors. A typical OLED consists of multiple organic functional layers and electrodes, with a total thickness usually on the sub-micrometer scale. In such a multilayer optical environment, radiation generated by dipole emitters in the emissive layer is strongly influenced by optical confinement and interference effects. In addition, refractive index discontinuities between functional layers cause a large portion of the emitted light to be trapped inside the device in the form of waveguide modes or surface plasmon polariton modes, so that only a small fraction can escape into air. As a result, accurate modeling of multilayer optical behavior, combined with micro- and nanostructure design to enhance light extraction efficiency (LEE), is a key challenge in OLED optical design. In this case, a 2D FDTD method is used to model an OLED device. By comparing structures without microstructures and with periodic microstructures (photonic crystals), the effect of microstructure design on LEE is evaluated.
In modern biosensing technologies, sensors based on optical resonant structures have attracted considerable attention due to their high sensitivity and label-free detection capability. As a representative nanoscale photonic element, resonant grating structures enable high-precision sensing by monitoring shifts in the resonance peaks of their reflection or transmission spectra in response to subtle variations in the surrounding refractive index. This property makes them highly attractive for applications in biomolecular recognition, environmental monitoring, and medical diagnostics. In this case study, following the work of *Cunningham et al.[^1]*, a representative resonant biosensor grating is modeled and simulated, and its optical response characteristics are analyzed.
In this case, we demonstrate a Y-branch splitter and how automatic geometric optimization can be achieved using parameterized structural descriptions. The algorithm automatically adjusts the control points of the parameterized structure, enhancing both design efficiency and device performance.
By employing a distinctive “concentric stepped ring” structure, the Fresnel lens decomposes the continuous surface of a conventional lens into multiple “annular micro-lenses,” each functioning as an independent refracting surface. This design dramatically reduces the lens thickness and mass while maintaining focusing or imaging performance comparable to that of a traditional convex lens. Because of this thin and lightweight architecture, Fresnel lenses are widely used in lighthouse illumination, projection systems, solar concentrators, and compact imaging devices—particularly in applications where high focusing efficiency is required under tight volume and cost constraints. In this case, a 2D FDTD simulation is performed for a Fresnel lens derived from a spherical lens profile, demonstrating its wavefront-shaping capability and characteristic phase behavior.
The blazed grating is a specially optimized diffractive structure designed to efficiently direct most of the incident light energy into a designated diffraction order by introducing a blaze angle on the grating surface. This significantly improves diffraction efficiency while suppressing unwanted orders. In this case study, an `FDTD` simulation is performed on a blazed grating to analyze its energy distribution among different diffraction orders.
The tapered-waveguide-type polarization converter achieves efficient polarization conversion by enabling smooth energy coupling between different polarization modes through a gradually varying waveguide cross-section along the propagation direction. This structure offers advantages such as broad bandwidth, low loss, and high tolerance to fabrication errors, making it widely used in optical communications, polarization multiplexing, and polarization control in silicon photonic chips. In this example, the FDE solver is first used to sweep the waveguide width and analyze the variation of the effective refractive index of the TM1 and TE0 modes, identifying the region where the two modes intersect to guide the design range of the tapered waveguide. Subsequently, the FDTD solver is employed to perform a three-dimensional simulation of the entire structure to calculate the light propagation and polarization conversion efficiency within the tapered waveguide.
The bull’s-eye aperture is a metallic subwavelength optical structure characterized by a central circular hole surrounded by periodically distributed concentric grooves. When incident light illuminates the metal surface, the concentric slits excite surface plasmon polaritons (SPPs) at specific wavelengths, which are re-radiated through the central aperture to the opposite side, resulting in strong transmission and significant field enhancement. In this case study, a bull’s-eye aperture fabricated on a silver film is simulated to demonstrate its characteristic field enhancement and directional radiation effects.
In FDTD simulations, obtaining the field distribution at locations far from a device usually requires expanding the simulation domain so that light can fully propagate to the target plane. While this approach is straightforward, it significantly increases computational cost and simulation time. This case presents a Grating Projection(GP)–based approach that can quickly obtain the distribution of fields propagating in homogeneous media at any specified location, and verifies its accuracy through comparison with FDTD simulation results.
In nonlinear optics, four-wave mixing (FWM) is a typical third-order nonlinear effect widely employed in areas such as all-optical signal processing, wavelength conversion, and the generation of new light sources. When light propagates through a material with Kerr nonlinearity, the nonlinear interaction of multi-frequency optical fields can generate new frequency components, achieving frequency mixing and energy transfer. This case demonstrates an FDTD simulation workflow for four-wave mixing based on a third-order nonlinear material.
