Contact Number
Email
 Enterprise WeChat
Enterprise WeChat WeChat Service Account
WeChat Service Account
 Wechat Channels
Wechat ChannelsSimWorks FDE is a powerful tool for researchers and engineers to solve problems of large-scale integrated planar optical waveguides, long-distance transmission devices, and various new types of optical fibers. We will briefly introduce the physical principles and key features.
Finite Difference Eigenmode (FDE) Solver calculates the spatial distributions and frequency characteristics of eigenmodes by solving Maxwell's equations on a cross-sectional mesh of waveguide-like structures. The basic principles of FDE are outlined as follows.
By adjusting the coefficients of frequency domain Maxwell's curl equation, it can be simplified to the following form:
According to the general form of the mode in the waveguide, the electric and magnetic fields can be written as and , which can be substituted into Maxwell's curl equation to obtain the expression of electromagnetic field component. For example, z-axis magnetic field component:
When linear expansion is done along the coordinate axis in space, the above equation can be transformed into the following matrix form:
The six matrix equations of the electromagnetic field components can be converted into the problem of solving the eigenvalues:
The matrix represents the coefficient matrix of the difference algorithm, the vector represents the electromagnetic field components to be solved, and the represents the propagation constant.
After 2D 'Yee cell' mesh is generated on the cross section of the waveguide structure, the material parameters, electric field and magnetic field can be reflected at each mesh point. In this algorithm, the sparse matrix technique is used to solve eigenvalue of the matrix, which generates the corresponding mode distribution and effective refractive index.
Mode Data
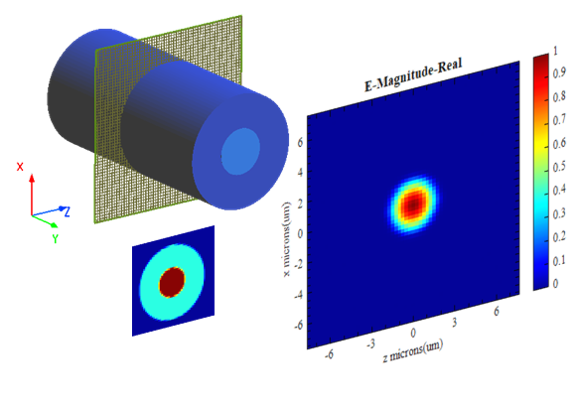
When the FDE solver type is selected as 2D Y normal, the simulation results are shown below.
Effective Index
Calculate the effective index of the mode using the following formula:
Where is the angular frequency, is the propagation constant of the mode, is the speed of light in vacuum, is group velocity of the mode, and is the wave vector in free space .
TE/TM Fraction
TE/TM fraction (TE/TM fraction(%)): The ratio between TE and TM energy distribution in a mode. Calculate it using the following formulas:
Wherein, is the electric field component along the propagation direction, is the magnetic field component along the propagation direction, and is the integrated area over the mode cross-section of an optical waveguide.
Loss
The transmission Loss (Loss(dB/cm)) of the mode is calculated as:
Wherein, is the imaginary part of the complex refractive index.
Mode coupling is used to calculate the field overlap and coupling efficiency between one input mode in one waveguide and all modes in the other waveguide. The basic principle of the mode coupling algorithm is outlined as follows.
For an interface input field , and output field , , the input and output power are respectively:
Since any field in a waveguide can be viewed as a combination of a basis consisting of a sequence of orthogonal modes, in the case of negligible reflection fields, the input and output fields can be expressed as follows:
The coefficients and are calculated by the following formulas:
The total power of the transmitted output field can thus be calculated as follows:
The mode coupling coefficient of the ith mode is calculated as follows:
The result of mode coupling shows how much power the field of the ith mode can be carried in a given input field. It should be noted that this algorithm is calculated based on the ideal case, and the calculation results may not be accurate when there is reflection or waveguide loss during transmission. For a detailed introduction, see Snyder and Love's "Optical Waveguide Theory".
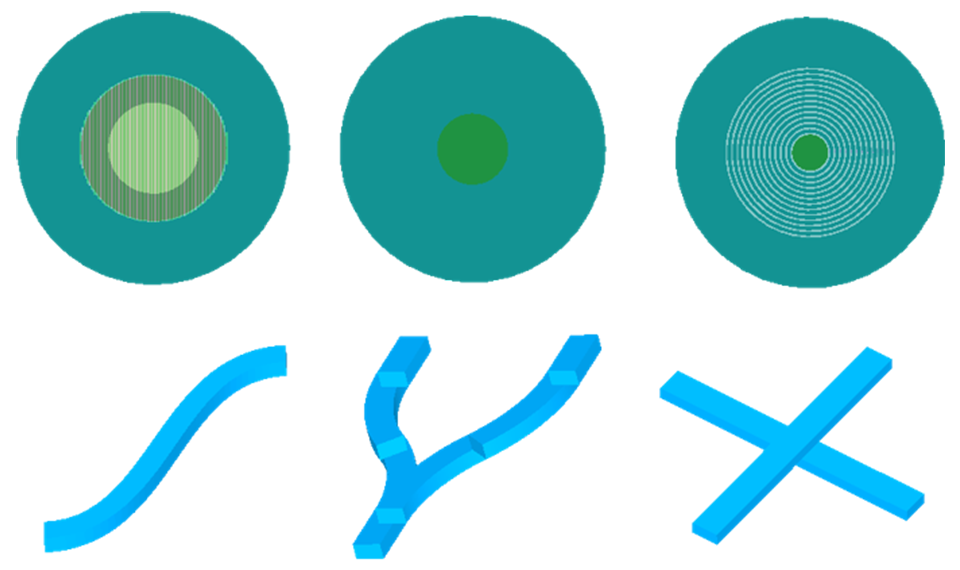
3D CAD interface and rich structure library
Mesh technology

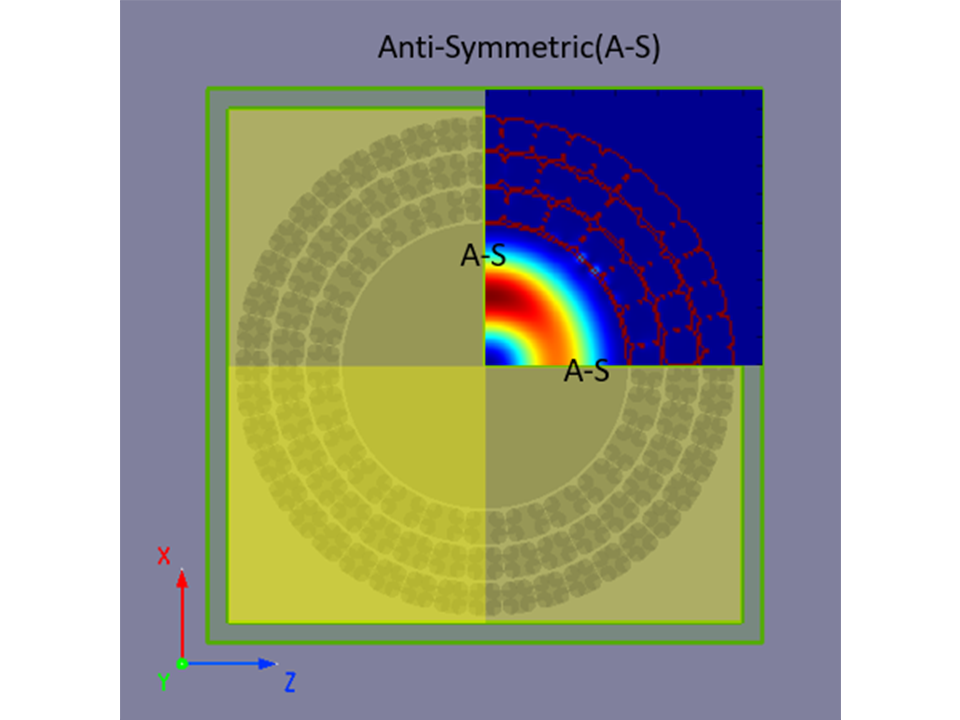
Boundary conditions
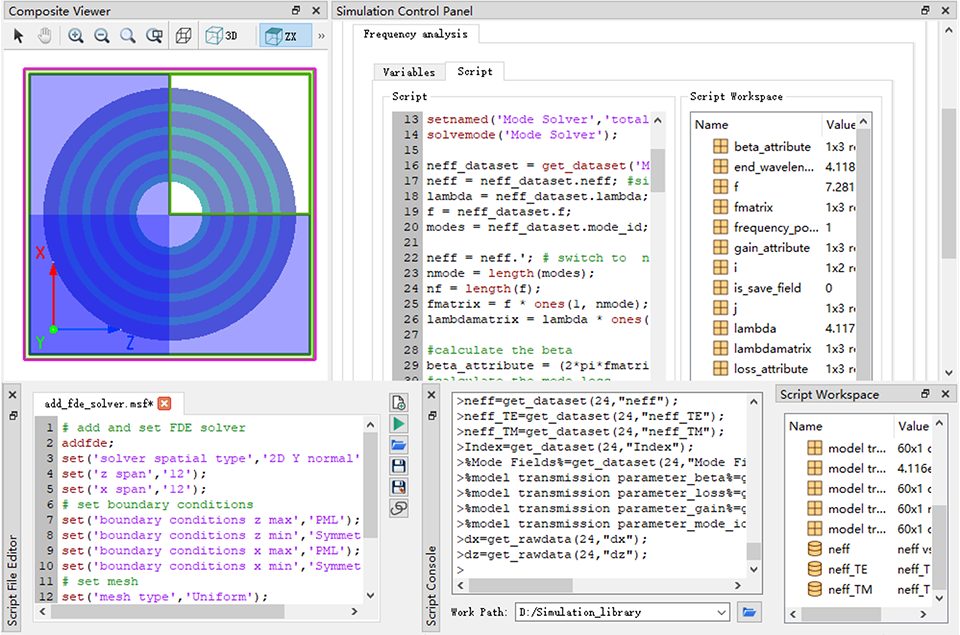
Frequency analysis
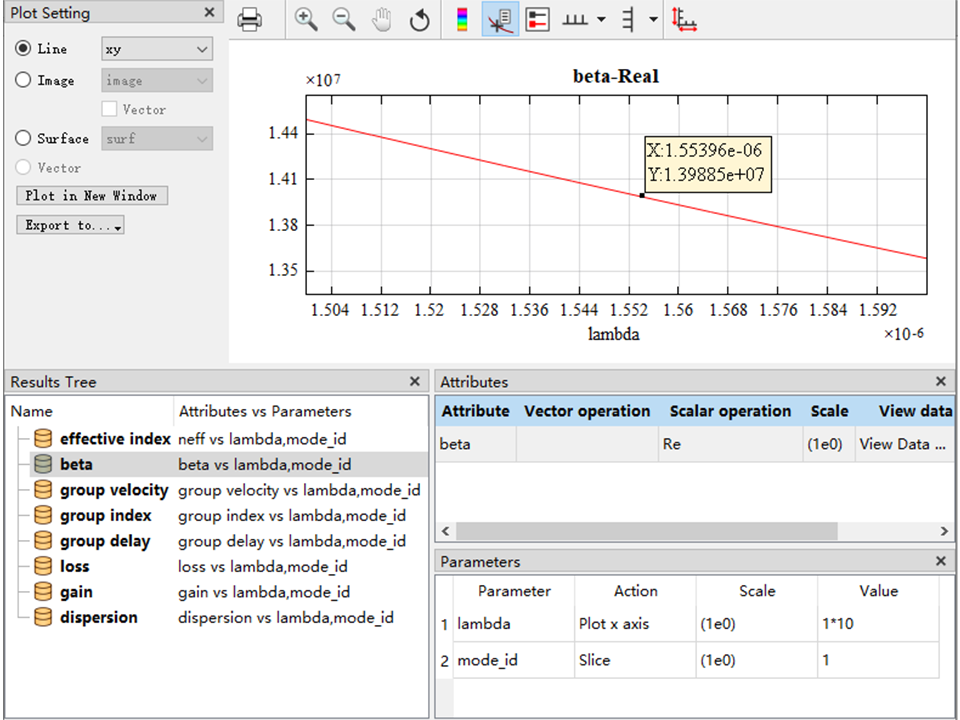
Script control
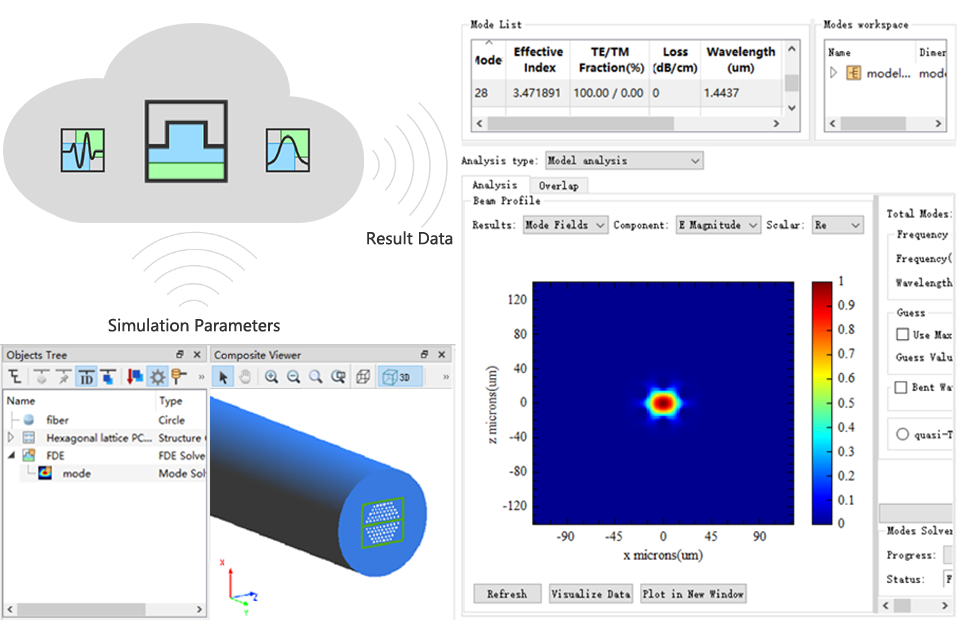
Computing power
Ultra-high computational accuracy
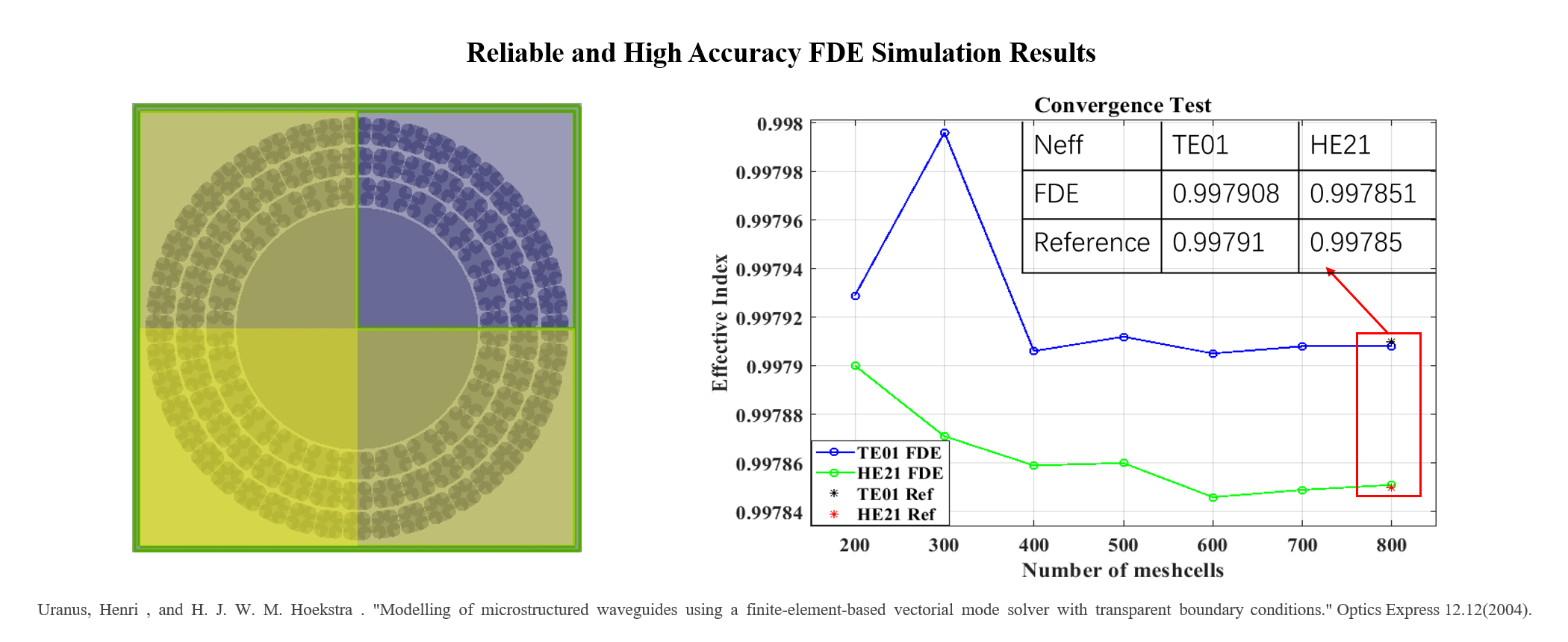
[1]Zhaoming Zhu and Thomas G. Brown, "Full-vectorial finite-difference analysis of microstructured optical fibers," Opt. Express 10, 853-864 (2002)