Preface #

In modern optical systems, diffractive optical elements have been widely applied in fields such as spectral dispersion, wavelength selection, and beam shaping due to their compact structure and functional versatility. Among them, the blazed grating is a specially optimized diffractive structure designed to efficiently direct most of the incident light energy into a designated diffraction order by introducing a blaze angle on the grating surface. This significantly improves diffraction efficiency while suppressing unwanted orders. In this case, an FDTD simulation is performed on a blazed grating to analyze its energy distribution among different diffraction orders.

Simulation settings #

Structure #

The blazed grating used in this case consists of a low-index substrate ($n=1.4$) and a high-index coating ($n=3.4$) with a thickness of $0.04\ \mu m$. The grating has a blaze angle of $30\degree$ and a period of $3\ \mu m$. The built-in Blaze grating structure group can be directly used to efficiently construct the grating geometry.

Solver settings #

The simulation uses 2D FDTD. Because the structure is periodic, the simulation region in the $Z$-direction is set to $3\ \mu m$, matching the grating period, and Bloch boundary conditions are applied in that direction so that simulating a single period yields the response of an infinite periodic grating.

To ensure accuracy, the simulation region must fully include portions of the structure where material or geometric variations are large, so that the electromagnetic fields are adequately resolved near the boundaries.

Source #

As shown in the figure below, the in-plane wave vector of the plane wave remains constant across different frequencies. Therefore, in broadband simulations, the actual incident angle varies with frequency.

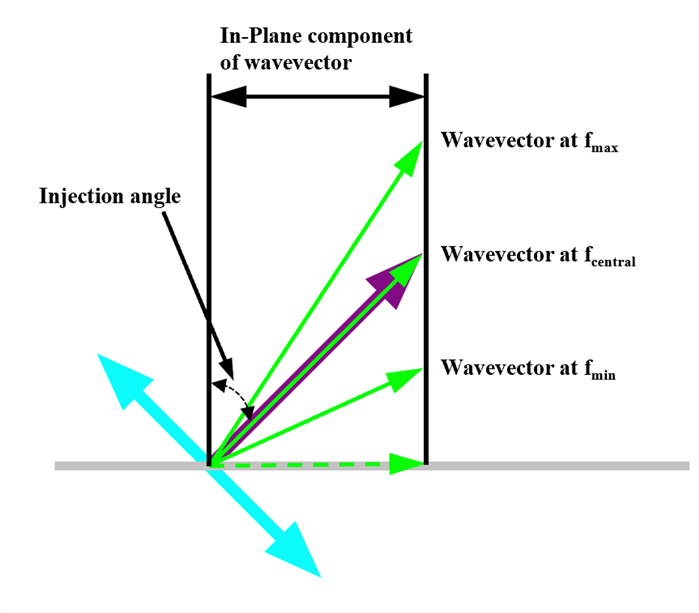
To avoid this issue, a single-frequency plane wave is employed, incident at an angle of $15\degree$. By sweeping the source over a range of frequencies, the grating’s diffraction behavior at different frequencies can be analyzed while keeping the incident angle constant.

Simulation results #

Run the blaze_grating.msf script to calculate the diffraction orders of reflection and transmission at a fixed wavelength, as well as the intensity of each diffraction order. The figure below shows the intensity of each diffraction order in reflection and transmission at a wavelength of $0.5\ \mu m$.

It can be seen that the energy in both reflection and transmission is mainly concentrated in a single diffraction order (the blaze order), while the energy in other diffraction orders is relatively small.

This indicates that the grating efficiently directs the incident light energy toward the target diffraction direction, exhibiting the typical characteristic of a blazed grating—energy concentrated in the blaze order.

Parameter analyses #

The attached project includes a predefined parameter sweep that sweeps the incident wavelength of the light source from $0.4\ \mu m$ to $0.7\ \mu m$. After the sweep, the total reflected energy distributed among all diffraction orders at each wavelength can be obtained, as shown in the figure below. The results show that the reflectance exhibits pronounced oscillations with wavelength, indicating that multiple diffraction orders exist within the structure at each wavelength.