Preface #

The Diffraction grating is a classic type of periodic optical element, widely used in fields such as spectroscopy, laser beam control, and beam splitting. Their functionality relies on spatially modulating the wavefront of incident light to generate a series of discrete diffraction orders in specific directions. Since a grating’s performance is governed by its diffraction-order energy distribution, precise quantification of this distribution becomes critical for design optimization.

In FDTD simulations, however, only near-field data is available from monitors placed close to the grating. To analyze the power carried by each diffraction order, this near-field data must be projected into the far field. To support this, the software provides a set of grating projection functions that can calculate key results such as the total number of diffraction orders, diffraction angles, and grating efficiency.

This case demonstrates how to use the grating projection functions in an FDTD simulation of a two-dimensional periodic grating, allowing for accurate evaluation of the energy distribution among diffraction orders and their corresponding efficiencies.

Simulation settings #

Device introduction #

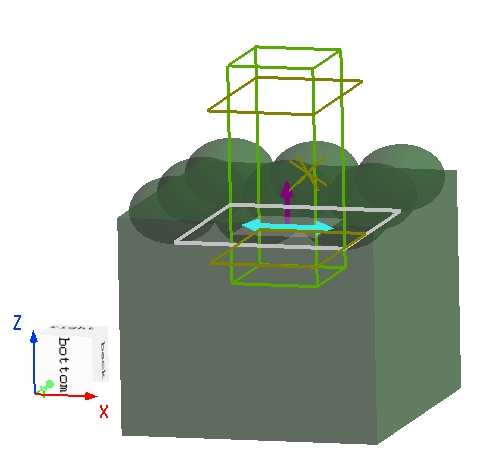
In this case study, the diffraction grating consists of a 2D array of semi-ellipsoidal particles placed on the top surface of a substrate with a refractive index of $n=2$, as illustrated below. A broadband plane wave is normally incident from within the substrate onto the surface grating, generating multiple diffraction orders in both the reflection and transmission regions. Bloch boundary conditions are applied along the $X, Y$ directions, allowing a single unit cell to represent an infinitely periodic grating in the simulation. To ensure accurate grating projection, the monitor’s span in the $X, Y$ directions must extend beyond the boundaries of the FDTD simulation region.

Simulation results #

Number of grating orders #

The figure below shows how the total number of diffraction orders varies with wavelength. As observed, shorter wavelengths result in more available diffraction orders, and there are more orders in the reflection direction than in transmission. This is because the substrate has a higher refractive index ($n=2$) compared to air, which shortens the effective wavelength within the substrate.

Fractional power into a specific diffraction order #

In practical scenarios, it is often necessary to calculate how much of the transmitted or reflected power is converted into a specific diffraction order:

$T(n,m)=\frac{Transmitted \space power \space to \space (n,m) \space order}{Total \space transmitted \space power}$

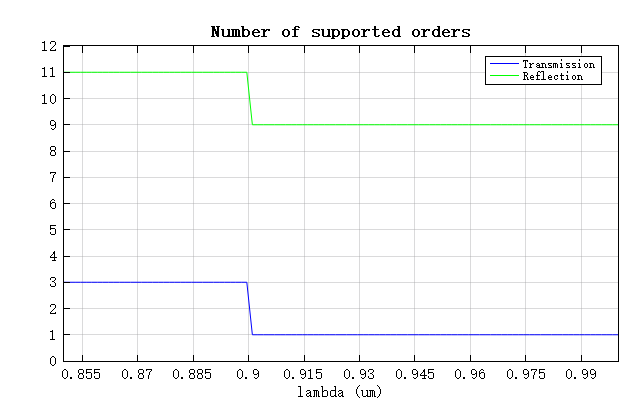
The figure below shows how the power fraction in the (0,0) diffraction order varies with wavelength for both transmission and reflection. In the transmitted (0,0) order, the transmission efficiency $T(0,0)$ becomes equal to the total transmission when the wavelength exceeds $0.9\mu m$, indicating that only one diffraction order exists in the transmission direction at those wavelengths—consistent with the results shown above. In contrast, the reflection efficiency $R(0,0)$ remains negligible across the entire wavelength range, implying that most of the reflected power is redistributed into higher-order diffraction modes.

Diffraction angle for a specific diffraction order #

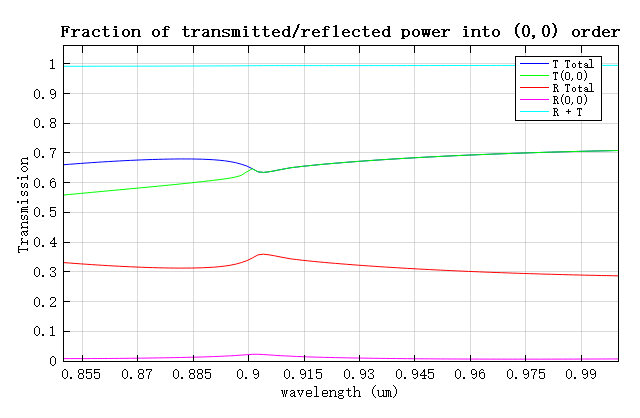
For a grating structure with a fixed period and incident angle, except for the (0,0) diffraction order, the diffraction angles of other orders are mainly determined by the wavelength. The figure below shows the variation trend of the diffraction angle of the transmitted (0,1) diffraction order with wavelength. At a wavelength of $0.85 \mu m$, this order propagates at an angle of approximately $70 \degree$. As the wavelength increases, $\theta$ gradually increases, indicating that the propagation direction of this order gradually approaches parallel to the grating period direction. When the wavelength exceeds $0.9 \mu m$, $\theta$ reaches $90 \degree$, and this diffraction order transitions into a non-propagating mode and disappears.

Diffraction efficiencies at a specific wavelength #

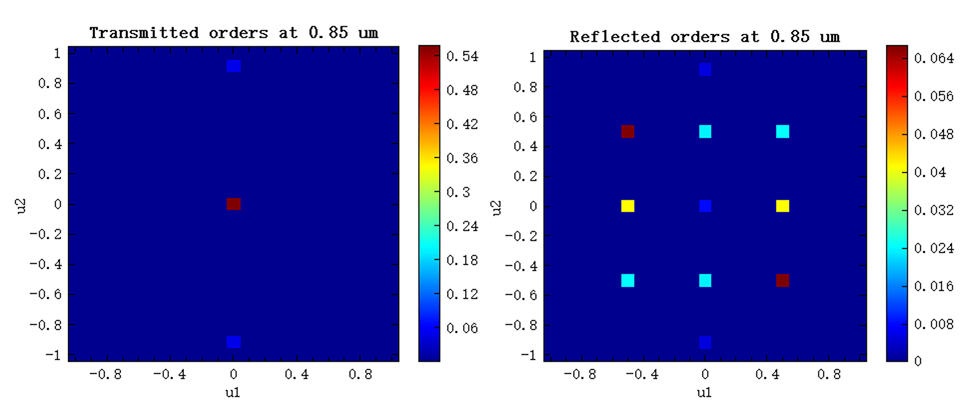
The figure below shows the distribution of diffraction efficiencies for transmitted and reflected diffraction orders at $0.85 \mu m$. The results are consistent with the above content. For example, there are 3 transmitted orders and 11 reflected orders, and more than 50% of the incident light energy is ultimately converted into the transmitted (0,0) diffraction order.