PSO Algorithm

This section describes the PSO algorithm.

The Particle Swarm Optimization (PSO) algorithm, initially used to simulate the social behavior of bird flocks or fish schools, is a stochastic optimization technique based on collective collaboration. It has been widely applied to address various optimization issues, including nanophotonics design ^[1][2]. The main purpose of the PSO algorithm is to find the optimal solution through collaboration and information sharing among individuals within the swarm.

Basic Principles of PSO Algorithm

In the process of seeking the optimal solution based on the PSO algorithm, each particle in the swarm exhibits both individual and collective behavior. They not only learn from the flight experience of their companions but also leverage their own flight experience to contribute to the search for the optimal solution. Each particle learns from two values: individual historical best value $p_{best}$ and swarm-based global best value $g_{best}$. Particles adjust their velocity and position based on these two values, and the quality of each position is determined by the fitness value. The fitness function serves as the objective function for optimization.

Particle and Velocity Initialization

In a $D$-dimensional objective search space, there is a particle swarm consisting of $N$ particles. Each particle is represented by a $D$-dimensional vector, and its spatial position can be expressed as:

$x_i=(x_{i1},x_{i2},... ,x_{iD}),i=1,2,3,...,N$

The spatial position of each particle in the swarm provides a solution to the objective optimization problem. By substituting it into the fitness function, the fitness value can be calculated and then used to measure the quality of the particle.
The flight velocity of the $i$th particle is also represented as a $D$-dimensional vector, which is expressed as:

$v_i=(v_{i1},v_{i2},... ,v_{iD}),i=1,2,3,...,N$

The average values of the positions and velocities of the particles are randomly generated within a specified range.

Individual Historical Best Value and Global Best Value

The position associated with the best fitness value experienced by the ith particle is referred to as its individual historical optimal position, which is expressed as:

$p_{besti}=(p_{besti1},p_{besti2},... ,p_{bestiD}),i=1,2,3,...,N$

The position associated with the best fitness value experienced by the entire particle swarm is referred to as the global optimal position, which is expressed as:

$g_{besti}=(g_{besti1},g_{besti2},... ,g_{bestiD}),i=1,2,3,...,N$

Particle Swarm Velocity and Position Update

For a particle swarm, the position update operation can be expressed by the velocity update formula and the position update formula.
The velocity update formula is:

$v_{ij}(t+1)=v_{ij}(t)+c_1r_1(p_{bestij}(t)-x_{ij}(t))+c_2r_2(g_{bestj}(t)-x_{ij}(t))$

The position update formula is:

$x_{ij}(t+1)=x_{ij}(t)+v_{ij}(t+1)$

Wherein, the subscript $j$ represents the $j$-th dimension of a particle; the subscript $i$ represents the $i$th particle; $t$ represents the current iteration count; $c_1$ and $c_2$ represent the acceleration constants, typically taken within the range of $(0,2)$; $r_1$ and $r_2$ represent independent random numbers, typically taken within the range of $[0,1]$. As shown in the above formulas, the constants $c_1$ and $c_2$ indicate that particles, through the combination of learning from individuals and the swarm, can leverage both individual and collective search experiences for their benefit.

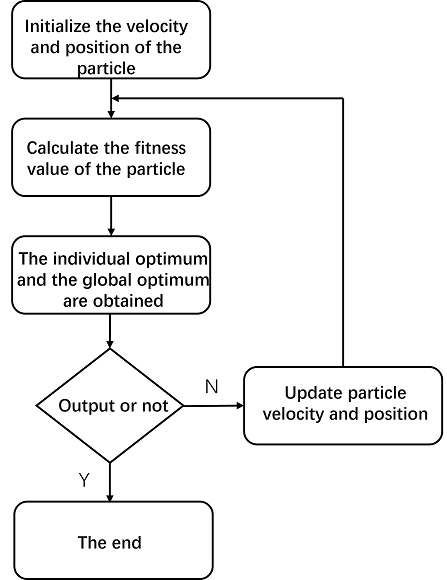
PSO Algorithm Process

The PSO algorithm is executed in the following steps:

1. Initialize the particle swarm parameters $c_1$ and $c_2$, set the boundary ranges of position and velocity, and initialize the velocities and positions of the particle swarm;
2. Calculate the objective values based on the objective function, and record each historical best value $p_{best}$ and the global best value $g_{best}$ respectively;
3. Update the velocities of the particle swarm using the velocity update formula, and constrain any velocities that exceed the boundary;
4. Update the position of the particle swarm using the position update formula, and constrain any positions that exceed the boundary;
5. Calculate the new objective values based on the objective function;
6. Compare each particle's new objective value with its historical best objective value, and take the former as the new historical best value $p_{best}$ if it is better;
7. Compare each particle's new objective value with the global best objective value achieved by the swarm, and take the former as the new global best value $g_{best}$ if it is better;
8. Determine whether the termination condition is met (the maximum number of iterations is reached). If so, output the optimal position. Otherwise, repeat Steps 3-8.

References

---

1. Robinson J , Rahmat-Samii Y .Particle Swarm Optimization in Electromagnetics. IEEE Trans. on Antennas and Propagation 52(2), 397-407[J].IEEE Transactions on Antennas and Propagation, 2004, 52(2):397-407. ↩︎

2. Parsopoulos K E , Vrahatis M N .Particle Swarm Optimization and Intelligence (Advances and Applications) || Applications in Bioinformatics and Medical Informatics[J]. 2010, 10.4018/978-1-61520-666-7(chapter 9):204-221. ↩︎