Graphene Material

This section describes the single-layer graphene materials.

Graphene Material

Graphene is an ultra-thin optical material (consisting of a single layer of atoms). Graphene is normally characterized by the surface conductivity $\sigma$ rather than permittivity $\varepsilon$ . Referring to the paper published by Hanson G W, when the presence of a magnetic field is ignored, the surface conductivity $\sigma(f, \mu_c, \Gamma, T)$ of a graphene material is expressed as:

$\sigma(f, \mu_c, \Gamma, T) = \sigma_{intra}(f, \mu_c, \Gamma, T) + \sigma_{inter}(f, \mu_c, \Gamma, T)$

On the right side of the equation for $\sigma(f, \mu_c, \Gamma, T)$ , the first term refers to intraband conductivity $\sigma_{intra}(f, \mu_c, \Gamma, T)$ , expressed as:

$\sigma_{intra}(f, \mu_c, \Gamma, T) = \frac{je^2}{\pi \hbar^2(2\pi f- j2\Gamma)}\int_0^\infty\xi(\frac{\partial f_d(\xi)}{\partial\xi}-\frac{\partial f_d(-\xi)}{\partial\xi})d\xi$

The second term refers to interband conductivity $\sigma_{inter}(f, \mu_c, \Gamma, T)$ , expressed as:

$\sigma_{inter}(f, \mu_c, \Gamma, T) = \frac{je^2(2\pi f - j2\Gamma)}{\pi \hbar^2}\int_0^\infty(\frac{f_d(\xi) - f_d(-\xi)}{(2\pi f - j2\Gamma)^2-4(\xi/\hbar^2)})d\xi$

Wherein, $f_d(\xi)$ represents the Fermi-Dirac distribution, expressed as: $f_d(\xi) = 1/[1 + e^{(\xi - \mu_c)/k_BT}]$ 。

In the above equation,

Symbol	Name	Units
$f$	Frequency	$Hz$
$\xi$	Energy state（ $\xi = \hbar \omega/2$ ）	$J$
$\Gamma$	Scattering rate	$eV$
$\mu_c$	Chemical potential	$eV$
$T$	Temperature	$K$
$e$	Electron charge	$C$
$\hbar$	Reduced Planck's constant	$\hbar = 6.62607015e−34 J\cdot s$

Among them, users are allowed to define the following four parameters:

Name	Symbol	Units	Range	Default	Description
Scattering rate	$\Gamma$	~	Real number, $\Gamma \geq1$	0.00051423	Scattering rate $\Gamma$ ， $\Gamma = 1/(2\tau)$ .
Chemical potential	$\mu_c$	eV	Real number, $\mu_c \geq0$	0.64
Temperature	$T$	$K$	Real number, $T\geq0$	300
Conductivity scaling	$c$	~	Real number, $c\geq0$	1	Conductivity scaling factor.

The above graphene surface conductivity equation is only valid for single-layer graphene materials. For multilayer graphene materials, the total conductivity can be achieved by adjusting the conductivity scaling factor based on the number of layers.

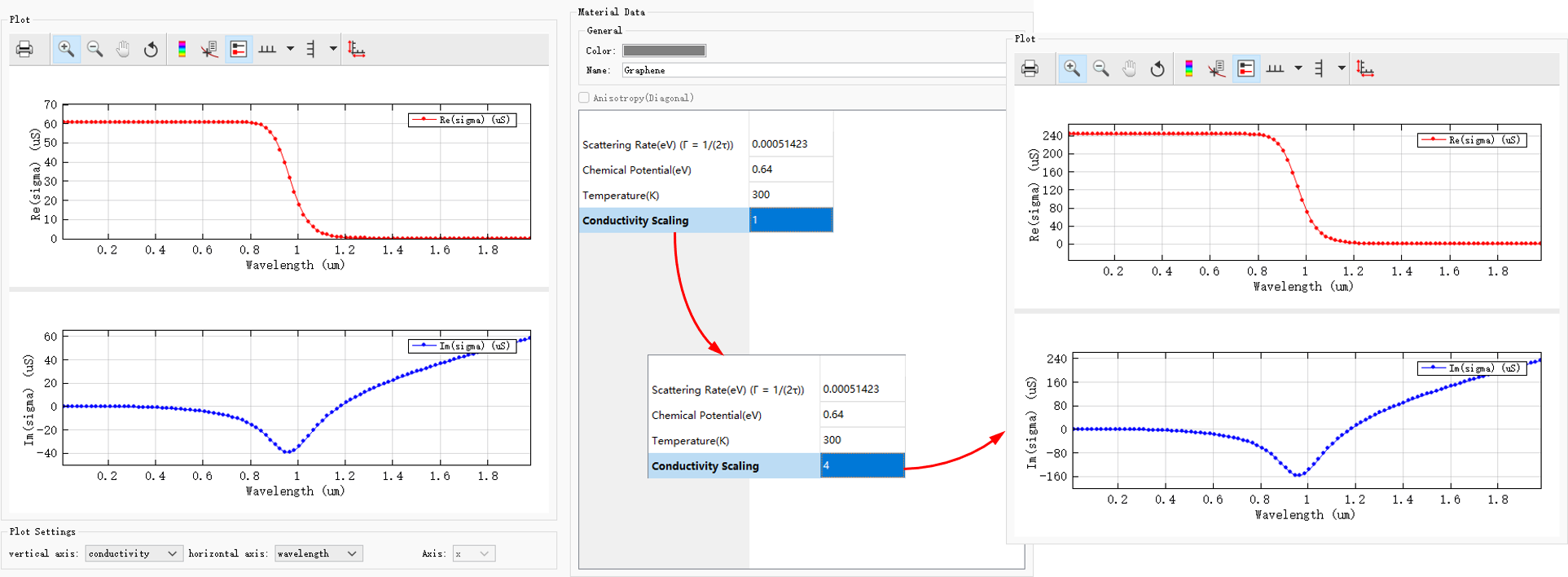
graphene_materialdata

Material Setting

In the Materials library window, you can add a graphene material model by selecting Add material>Add new material>Add graphene, and modify the material parameters of the graphene model in the pop-up editing interface to create the desired graphene material model (Please refer to the above picture). Switching to the model fitting , users can observe whether the material fitting model fits correctly in the corresponding band.

graphene_fittingplot

More Information

Graphene material models can only be defined with 2D structures.
Graphene materials do not support anisotropy.
Since graphene materials are special 2D materials, in contrast to common materials, accurate simulations of graphene can be achieved without requiring a high-resolution mesh specifically applied to the graphene structure.

Due to its unique optical, electrical and mechanical properties, graphene has become a major focus of research in various fields. Here is a typical case in Exciting surface plasmons in graphene applications.

Case: Graphene-Based Tunable Terahertz Metamaterials

Graphene is a single-layer carbon material that is only one atom thick. It can be used in nanoscale plasma systems due to its unique physical properties. Light can be manipulated and controlled by adjusting the electrostatic doping or Fermi level to excite plasmon waves in single-layer graphene. For details, see Graphene Metamaterials.

[1] Hanson G W. Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene[J]. Journal of Applied Physics, 2008, 103(6): 064302.
[2] Falkovsky L A. Optical properties of graphene[J]. Journal of Physics Conference Series. 2008, 129: 012004.

Graphene Material