FDFP Monitor Setting

This section describes Frequency Domain Field and Power (FDFP) monitor.

Use FDFP monitor to calculate data of electromagnetic field in frequency domain in a specified geometric space.

Select FDFP monitor from the solver tab, create an FDFP monitor in the Composite viewer, and set relevant parameters in the automatically pop-up Properties Editing interface.

Computing and Processing of FDFP Monitor

For physical variables defined in time domain, space domain, and frequency domain, they are interconnected through Fourier transform. FDFP monitor can convert time domain signals into frequency domain signals. Therefore, FDFP monitor is capable of not only recording data but also computing and processing data.

Electric Field and Magnetic Field

Electric Field

The electric field in the frequency domain returned by the FDFP monitor is given by the following formula:

$\boldsymbol{E}(\omega) = \int \boldsymbol{E}(t) e^{-i\omega t}dt$

wherein, $\boldsymbol{E}(t)$ is electric field in the time domain, $e^{-i\omega t}$ is a complex-exponential function, and $t$ is time.

Magnetic Field

The magnetic field in frequency domain returned by the FDFP monitor is given by the following formula:

$\boldsymbol{H}(\omega) = \int \boldsymbol{H}(t) e^{-i\omega t}dt$

wherein, $\boldsymbol{H}(t)$ is magnetic field in time domain, $e^{-i\omega t}$ is a complex-exponential function, and $t$ is time.

Energy, Power, and Transmissivity

Poynting Vector

The Poynting vector of the FDFP monitor is given by the following formula:

$\boldsymbol{P}(\omega) = \boldsymbol{E}(\omega)\times \boldsymbol{H}(\omega)^*$

$\boldsymbol{E}(\omega)$ is electric field in frequency domain, and $~\boldsymbol{H}(\omega)^*~$ is a conjugate complex number of magnetic field in frequency domain.

Power

Power of the FDFP monitor is calculated by the following formula:

$power = \int \boldsymbol{P}(\omega) \cdot d\boldsymbol{s}$

$\boldsymbol{P}(\omega)$ is a Poynting vector, and $d\boldsymbol{s}$ is a surface normal direction.

Transmissivity

Transmissivity of the FDFP monitor is calculated by the following formula:

$T(\omega) = \frac{0.5\int Re(\boldsymbol{P}(\omega))\cdot d\boldsymbol{s}}{source power(\omega)}$

$\boldsymbol{P}(\omega)$ is a Poynting vector, $source power(\omega)$ is an incident power, and $d\boldsymbol{s}$ is a surface normal direction.

FDFP Monitor Setting

General Setting

General tab is used for general settings of the FDFP monitor.

Data Monitoring

Name	Description
Data type	Record data type, which is Frequency-domain by default. This is a read-only parameter.
Spatial interpolation	Select types of spatial interpolation from drop-down menu: None: No spatial interpolation is performed; record electromagnetic field components at different locations within the Yee cell; Mesh cell: Record each component of the electric and magnetic fields at different locations within the Yee cell. To accurately calculate the Poynting vector and electromagnetic energy density, you can choose to interpolate field components to the same location on the Yee cell. After selecting this option for spatial interpolation, field values are interpolated to the nearest Yee cell boundary.
Record data in PML	Record data in the PML region, which is an advanced setting and not checked by default.

Components

Name	Description
Components	Electromagnetic field components: Ex, Ey, Ez; Hx, Hy, Hz; Poynting vectors: Px, Py, Pz.

Frequency Sampling

Name	Description
Min sampling per cycle	Minimum amount of sampling per cycle; used to set number of sampling points per cycle, with default value of 2.
Desired sampling	A parameter used to control sampling density, specifying sampling interval or step size during the simulation process.
Nyquist limit	To accurately reconstruct a continuous time signal, signal must be sampled at a rate not less than twice the highest frequency of the signal being analyzed.
Sampling frequency	The actual sampling frequency is the frequency used for discrete Fourier transforms. Sampling frequency should be at least twice the highest frequency of the signal being analyzed, to comply with Nyquist limit requirements.
Sample time(per # of dt)	Time interval of sampling during simulation, that is, after how many time steps a sample is taken from the field.

Space Sampling

Name	Description
Per # of dx/dy/dz	Interval at which sampling is performed in the X/Y/Z direction during the simulation process, that is, after how many discretization steps a sampling is conducted.

Geometric Dimensions

Geometry is the tab for setting geometric dimensions of the FDFP monitor. Please refer to geometric dimensions setting of the monitor.

Wavelength/Frequency

Frequency Settings

Frequency settings tab is used to set up bandwidth range and number of frequency points for FDFP monitor.

• Base on source setting

When Base on source setting is checked, the wavelength/frequency range option on the tab exhibits wavelength/frequency range of the light source, and wavelength/frequency range setting tab is in read-only mode.

When Base on source setting is unchecked, wavelength/frequency range option on the tab can be customized.

• Edit simplified

Edit simplified settings is a simplified way to customize wavelength range for the monitor.

• Edit complicated

Edit complicated settings is a complicated way to customize wavelength/frequency range for the monitor.

Apodization

The Fourier transform is used to study the correlation between the entire time domain and frequency domain. During simulation, it is not feasible to measure and compute infinitely long signals; instead, finite segments in time domain are taken for analysis. Different window functions can be applied to apodize signals, and these window functions are used to smoothly taper signals at the edges of the sampling region to zero.

Name	Description
Apodization type	Select apodization type by drop-down.
Apodization function	Select the type of apodization window function by drop-down.
Apodization center	The center position of the window function, which is the point where the time-domain signal begins to attenuate.
Apodization time width	Control width of the window function in time domain, which is duration from window being enabled to complete attenuation. A shorter width in time domain will result in faster attenuation rate, while a longer width in time domain will produce slower attenuation.

There are three apodization types:

Name	Description
None	No apodization applied to time domain signal.
Full	Uniform attenuation of time domain signal in the entire response region. After a time-domain signal is converted to a frequency-domain one, only the data at the window is preserved.
Start	Attenuated from starting position of time domain signal, and used to filter front-end data in time domain.
End	Attenuated from ending position of time-domain signal, and used to filter data in time domain at the simulation back-end.

Software includes nine types of built-in window functions, each with different characteristics. Users can select the appropriate window function based on their actual needs:

Gaussian: Exhibit a Gaussian distribution in time domain and have smooth attenuation characteristics. The Gaussian window function has a wider mainlobe in the frequency domain, resulting in lower frequency resolution. It is expressed as:

$\omega(t)={e}^{-\frac{t^2}{2 {\sigma}^2}}$

wherein, $\sigma$ is a standard deviation parameter that controls window bandwidth, and $t$ is time.

Bartlett: Appear a triangular shape in time domain and has smooth attenuation characteristics. Its amplitude gradually decreases from center of the window towards both ends, resembling a symmetric triangular Bartlett window function. It has a wider mainlobe and relatively higher sidelobe power in the frequency domain; therefore, when better spectral resolution and lower sidelobe leakage are required, other types of window functions, such as the Hanning, Hamming, or Blackman windows, may need to be considered. It is expressed as:

$\omega(t)=1-\frac{|t|}{T}$

wherein, $t$ is time, and $T$ is a window width in time domain.

Blackman: Exhibits smooth attenuation characteristics in time domain, and includes a primary cosine term and a secondary cosine term, providing better sidelobe suppression and spectral resolution in frequency domain. It is expressed as:

$\omega(t) = 0.42 - 0.5 \cos\left(\frac{2\pi t}{T}\right) + 0.08 \cos\left(\frac{4\pi t}{T}\right)$

wherein, $t$ is time, and $T$ is a window width in time domain.

Connes: Has smooth curved amplitude distribution in time domain. Compared to other window functions, it has a slower amplitude attenuation at start and end positions. It is expressed as:

$\omega(t) = \left(1 - \frac{t^2}{(\frac{T}{2})^2}\right)^2$

wherein, $t$ is time, and $T$ is a window width in time domain.

Cosine: Has a periodically changed amplitude distribution in time domain, from minimum to maximum, and then back to minimum. This periodic change results in a uniform amplitude distribution of time-domain signal. It is expressed as:

$\omega(t) = cos\left(\frac{\pi t}{T}\right)$

wherein, $t$ is time, and $T$ is a window width in time domain.

Hanning: Exhibits smooth attenuation characteristics in time domain, similar to a cosine waveform. Advantage of the Hanning window function is its smoothly attenuated shape helps in reduction of spectral leakage, providing better spectral resolution. Disadvantage is smooth attenuation characteristics in time domain lead to an increase in mainlobe width in frequency domain. It is expressed as:

$\omega(t)=0.5-0.5cos(\frac{2\pi t}{T})$

wherein $t$ is time, and $T$ is a window width in time domain.

Hamming: Exhibits smooth attenuation characteristics similar to a cosine waveform in time domain, like the Hanning window function. The Hamming window function has lower sidelobe power and spectral leakage. Compared to the Hanning window function, Hamming window function has quicker attenuation at both ends of the window. The Hamming window function provides better sidelobe suppression in spectral analysis, but also results in a wider mainlobe. It is expressed as:

$\omega(t) =0.54 - 0.46cos(\frac{2\pi t}{T})$

wherein, $t$ is time, and $T$ is a window width in time domain.

Welch: Exhibits a parabolic shape in time domain, and has better sidelobe suppression. It is similar to the Bartlett window function, but has a faster attenuation rate at the ends of the window. It is expressed as:

$\omega(t) = 1 - \frac{t^2}{(\frac{T}{2})^2}$

$t$ is time, and $T$ is a window width in time domain.

Uniform: A rectangular window function, with a constant value of 1 taken inside the window and a value of 0 taken outside the window. Advantage of the function is the mainlobe is concentrated, while disadvantage is lack of smooth attenuation characteristics, resulting in larger spectral leakage and sidelobe power. It is expressed as:

$\omega(t)=\begin{cases} 1 & -\frac{T}{2}\leq t \leq \frac{T}{2} \\ 0 & otherwise \\ \end{cases}$

wherein, $t$ is time, and $T$ is a window width in time domain.

Mode Expansion

Mode expansion is used to set up mode expansion of FDFP monitor. For specific setting details, please refer to FDFP Monitor Mode Expansion.

Data Visualizer

Use FDFP monitor to save frequency domain field datasets obtained from time domain simulation. Returned data includes:

• E: relation between electric field and frequency (wavelength);
• H: relation between magnetic field and frequency (wavelength);
• P: relation between Poynting vector and frequency (wavelength);
• Power: relation between power and frequency (wavelength);
• T: relation between transmissivity and frequency (wavelength).

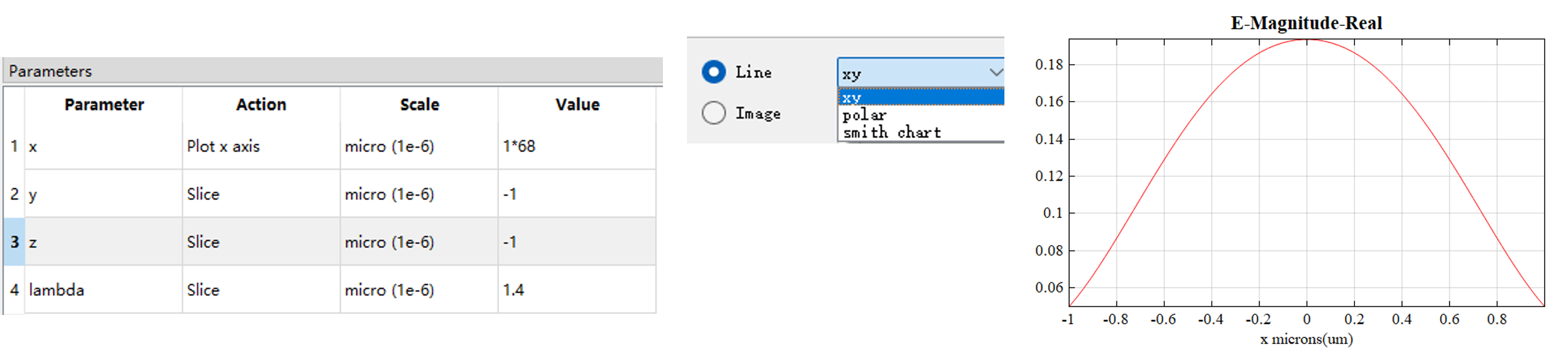
View field distribution in frequency domain in Data visualizer of the FDFP monitor, with specific operations as shown in the Figures below:

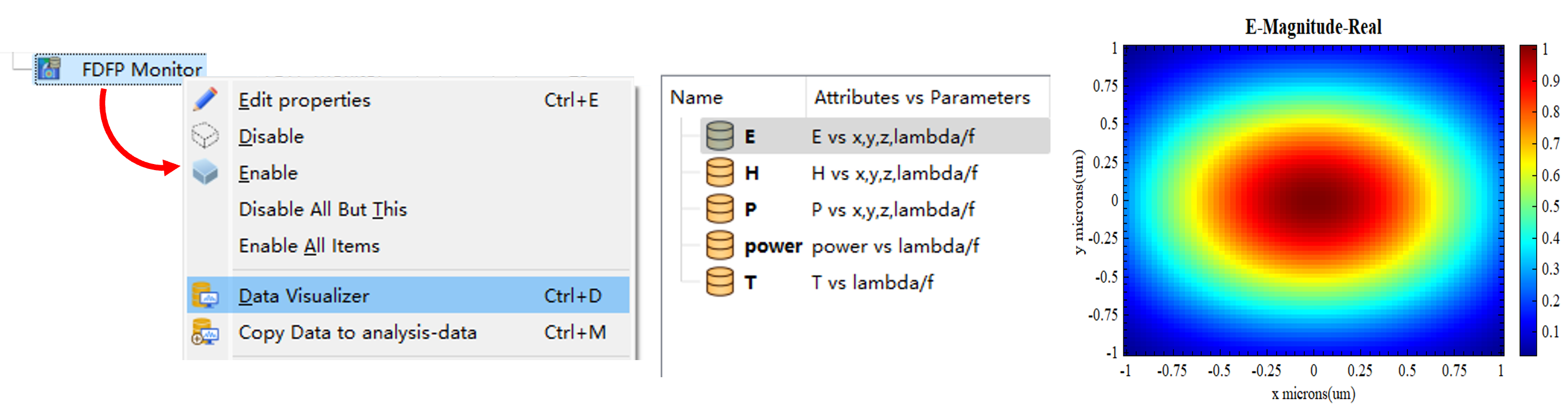
Perform operations such as selection, plotting, and saving of data in the data visualization interface. For more details, see Data Visualizer.

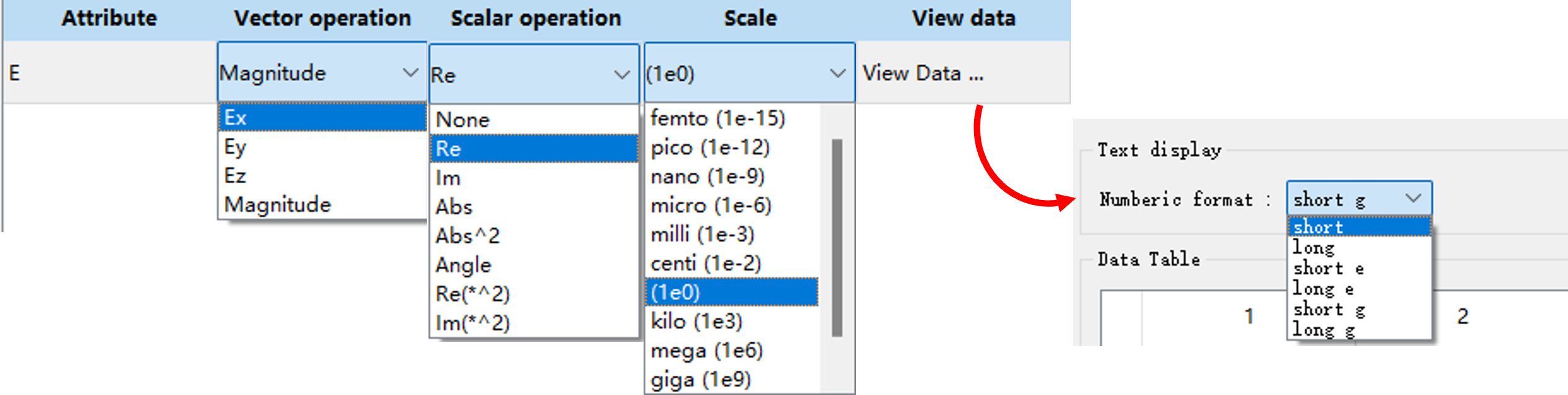
For instance, to view the real part of the $E_x$ component, settings and results for Attributes are shown as in the Figure below:

Plot a one-dimensional dataset as a 1D line plot: