Boundary Conditions Settings

This section describes boundary conditions for solvers.

Boundary conditions are one of the important settings for solvers. Selecting appropriate boundary conditions can significantly improve simulation efficiency and accuracy.

Boundary Conditions

Boundary conditions are classified into the following types:

Name	Description
PML	Perfect match layer. PML boundary conditions can effectively absorb incident or reflected electromagnetic waves from the boundaries of the computing region, preventing wave reflection.
Periodic	Periodic boundary. Calculate the response of an entire periodic system by simulating a single unit.
Bloch	Bloch boundary. If the structure exhibits periodicity, it is applicable to periodic sources incident at a designated angle and single wavelength.
PEC	Perfect electrical conductor. The electric field component parallel to the PEC boundary is zero; the magnetic field component perpendicular to the PEC boundary is also zero. The PEC boundary has total reflection properties.
PMC	Perfect magnetic conductor. The magnetic field component parallel to the PMC boundary is zero; the electric field component perpendicular to the PMC boundary is also zero. The PMC boundary has total reflection properties.
Symmetric/Anti-symmetric	Symmetric/anti-symmetric boundary. When setting a symmetric/anti-symmetric boundary, the electromagnetic field in the simulation region also meets the requirements of the symmetric/anti-symmetric configuration.

PML

PML Effects

Here demonstrates the actual effects of PML.

Use the FDFP monitor to record the attenuation trend of the field values passing through the PML boundary with distance.

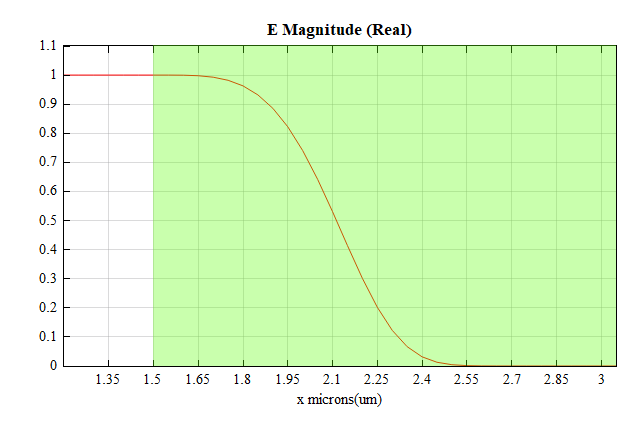
As shown in the figure, with the layer-by-layer absorption of PML, the optical field quickly attenuates to a negligible level after light is incident on the PML boundary.

PML and Structure

The software employs a stretched PML. For structures passing through the PML boundary, see the boundary section on the Structure page.

In the FDTD attribute boundary condition tab, there is an option labeled Extend Structure through PML, as shown in the following figure. This option is enabled by default.

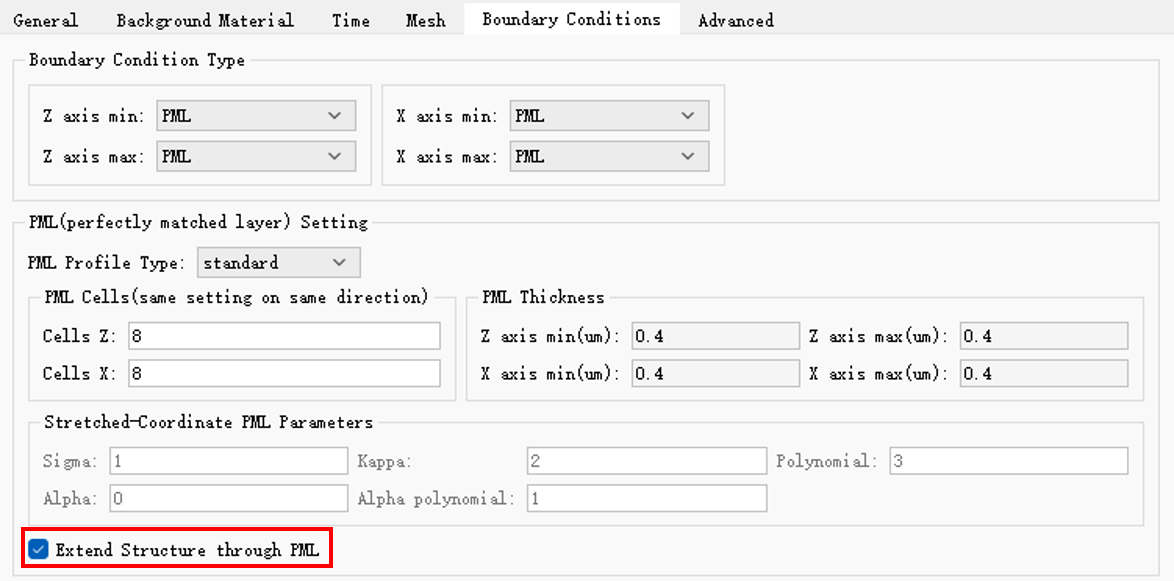
extend_structure_through_PML

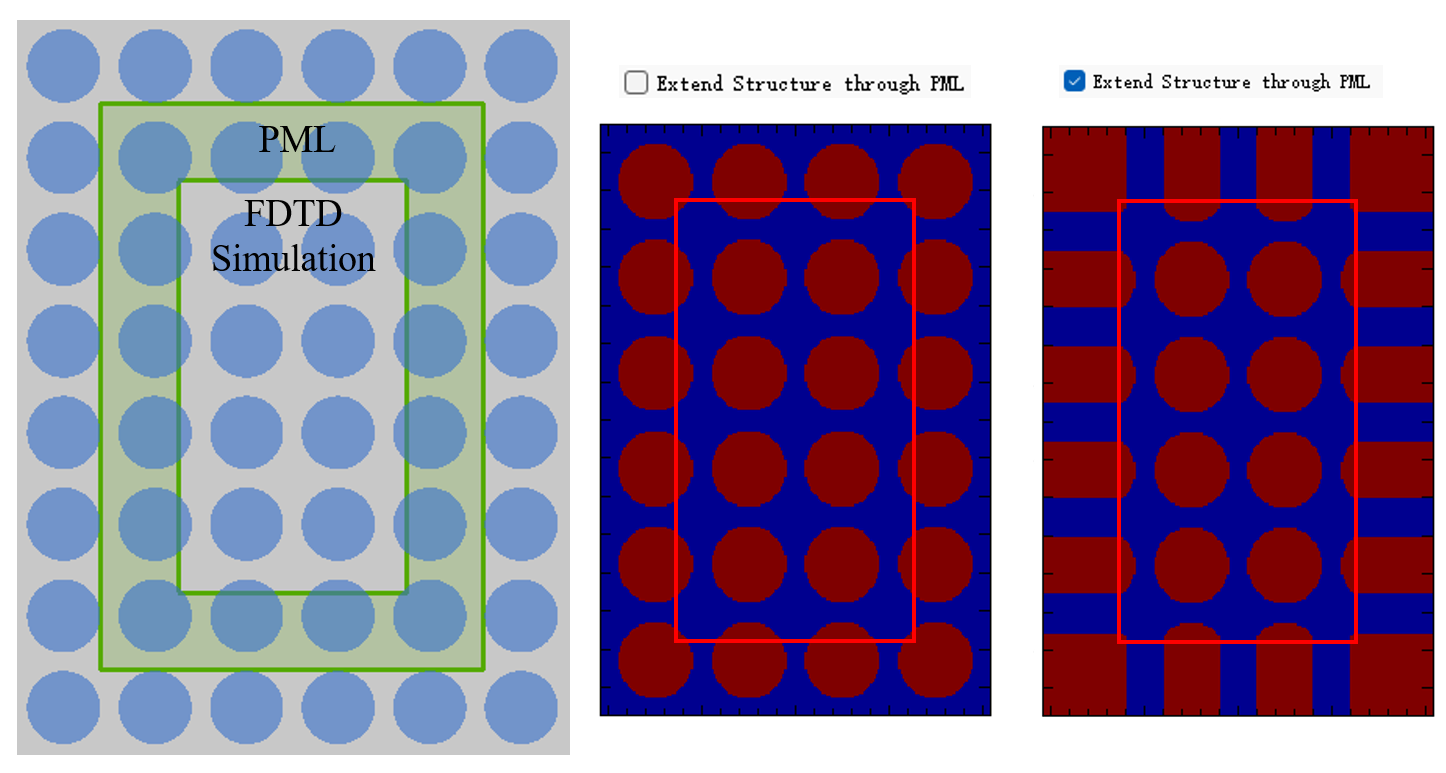
When this option is checked, the software will automatically extend the structure that touches the inner PML boundary in the direction normal to the boundary. For multi-layer flat structures, selecting this option will reduce reflection between the simulation area and boundaries, which enhances the absorption performance of PML. Therefore, we suggest that users check this option to reduce the reflection of stray light.

PML_rectangle

However, for periodic structures such as photonic crystals, this option should be disabled to avoid losing the periodicity of the photonic crystal when the crystal structure that contacts the inner boundary is unintentionally expanded.

PML_PC

PML, Source, and Monitor

The spatial dimensions of sources and monitors are allowed to exceed the simulation region. However, it is important to note:

By default, the portion of the source that extends beyond the simulation region is invalid;
By default, the monitor does not record data beyond the simulation region;
The monitor offers a setting for recording PML fields: Record data in PML.

PML Configuration Type

The software includes three predefined PML configurations as built-in options, which are used to adjust and optimize the performance of the absorbing layer. Users can select the desired PML configuration from the drop-down list in the PML profile type tab.

Name	Description
Standard	This configuration offers effective overall absorption with fewer layers. It is recommended to prioritize this option. The standard configuration is suitable for simulation projects without structure passing through the PML region.
Stabilized	Numerical instability may occur when material boundaries pass through the PML layer or the source is incident on the PML layer at a large angle. Using the stabilized configuration can prevent light divergence within the PML layer. The stabilized configuration primarily enhances stability by adjusting the PML parameters and increasing the number of PML layers. Achieving better absorption requires more PML layers, which, in turn, increases calculation complexity and resource requirements.
Custom	This option allows users to enter PML parameter values. The default values for the custom configuration are the parameter values used in the standard configuration. It is recommended that users fully understand the principle of PML before attempting to make this setting.

PML Settings

For the Custom type, the following user-defined parameters are available:

Name	Description
Cells Z/X/Y	The number of PML cells.
Sigma	The conductivity of the PML layer. It is used to adjust the absorption capability of the PML layer for electromagnetic waves.
Alpha	The loss coefficient of the PML layer. It is used to reduce reflection of low-frequency signals from the PML surface.
Kappa	Unitless.
Polynomial	Use polynomial functions to describe the variations of Kappa and Sigma.
Alpha polynomial	Use polynomial functions to describe the variations of Alpha.

For the Standard or Stabilized type, only one user-defined parameter is available:

Name	Description
Cells Z/X/Y	The number of PML cells.

Periodic Boundary

For periodic/Bloch boundary in the same direction (X/Y/Z), the upper and lower boundary conditions must be consistent.
In a project where periodic boundary conditions are employed, all elements, including the structure and electromagnetic field, should exhibit periodicity. Note that the use of periodic boundary conditions is not supported in the following two cases:
- A plane wave is incident on a periodic structure at a specific angle. In this case, the source is subject to a phase shift, requiring the use of the Bloch boundary;
- A periodic structure is excited by a single incoherent dipole source. In this case, the system is non-periodic.

Bloch

Bloch boundary conditions are primarily used in projects where a plane wave is incident on a periodic structure at a specific angle. The Bloch boundary is used to correct the phase of the field at one boundary and incident it into another.

Expressed as:

$\vec{E}_{x_{max}} = e^{-ia_{x} \ {k}_{x} } \vec{E}_{x_{min}}$

$\vec{E}_{x_{max}} = e^{ ia*{x} \ {k}*{x} } \vec{E}_{x_{min}}$

wherein, $k_x$ represents the Bloch wave vector, and $a_{x}$ represents the lattice translation vector.

In FDTD simulations, the Sine-cosine method is used to implement the Bloch boundary conditions for a single frequency point. For broadband simulations, it is necessary to use the built-in sweeping feature provided by the software to obtain accurate results. For details, see Sweep.

For the Bloch boundary, the Using source angle option is checked by default to enable calculation of the Bloch wave vector based on the source angle. If this option is unchecked, the Bloch wave vector needs to be defined by users.

Name	Description
kx/ky/kz	The component of the wave vector K along the x/y/z direction.

In the analysis of band structures, the sweep frequency and Bloch wave vector are interdependent and indispensable settings.

PEC

With the PEC boundary conditions, the electric field component parallel to the PEC boundary is zero, and the magnetic field component perpendicular to the PEC boundary is also zero. That is,

PMC

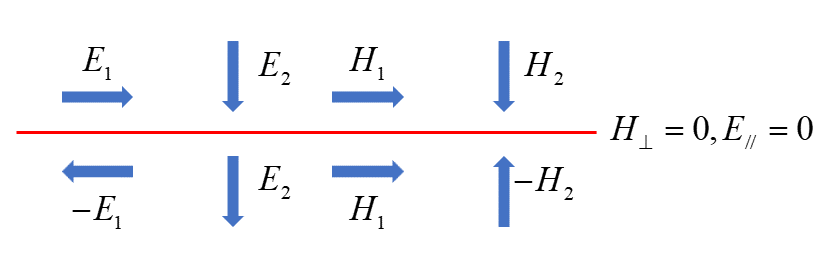
With the PMC boundary conditions, the magnetic field component parallel to the PMC boundary is zero, and the electric field component perpendicular to the PMC boundary is also zero.That is,

Symmetry/Anti-Symmetry

Electromagnetic Field at Symmetric/Anti-Symmetric Boundary

Electric fields at the symmetric/anti-symmetric boundary:

Magnetic fields at the symmetric/antisymmetric boundary:

Symmetric/Anti-Symmetric Boundary Settings

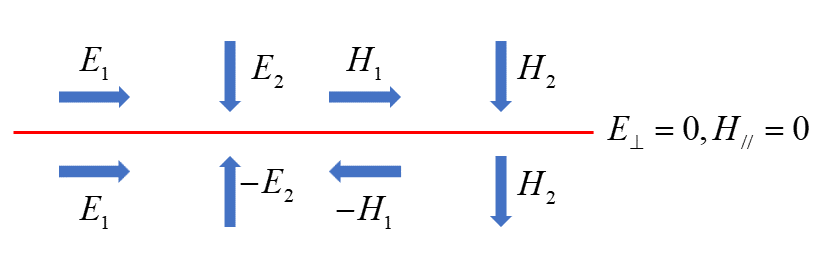
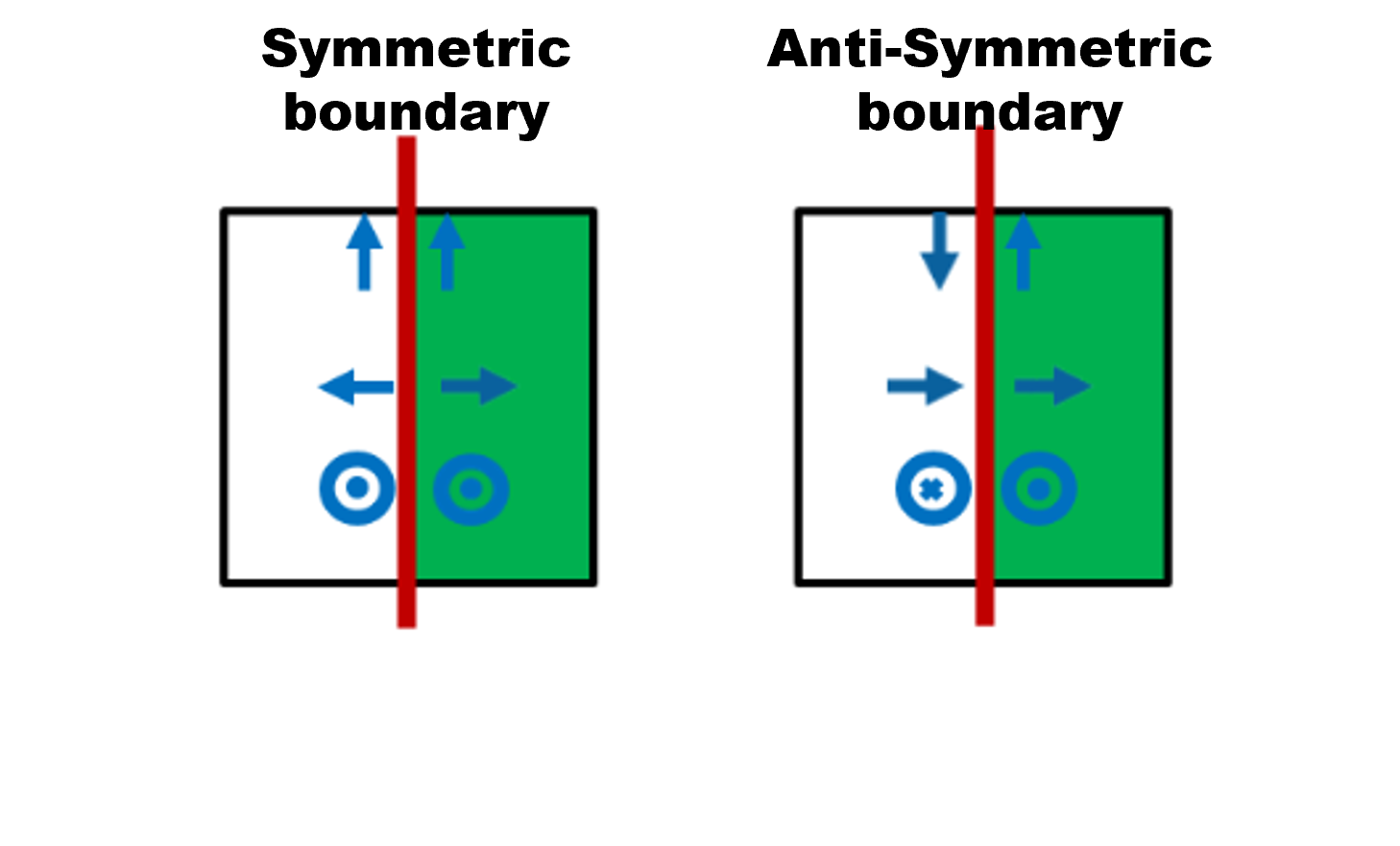
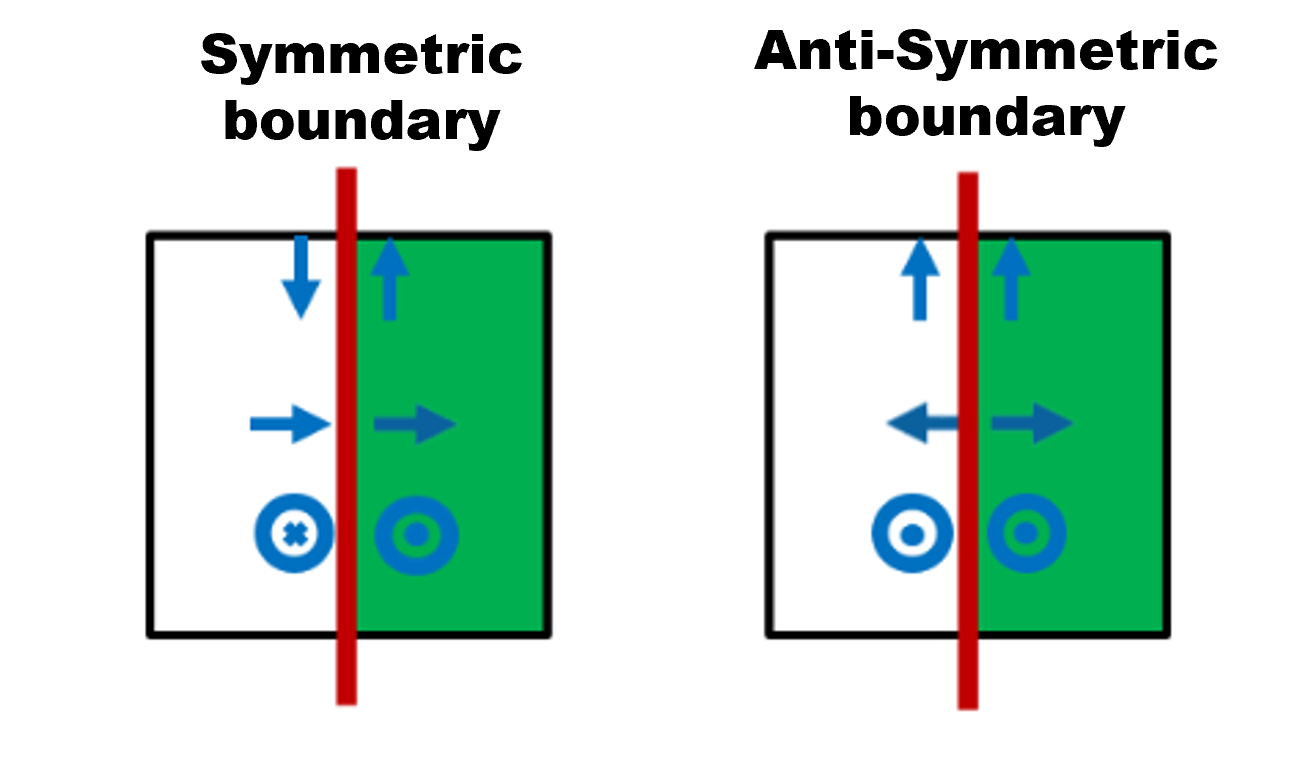
The symmetry/anti-symmetry boundary requires not only symmetry in the physical structure (including geometry and materials), but also symmetry in the field distribution of the source. Leveraging this symmetry can reduce the calculation space by half in each direction and greatly speed up the simulation.

Symmetry/Anti-Symmetry Usage Tips

For devices, the symmetry in the structure and simulation region is mandatory;
The source must be properly positioned to meet the symmetric/anti-symmetric boundary.

Periodic Boundary and Symmetric/Anti-Symmetric Boundary

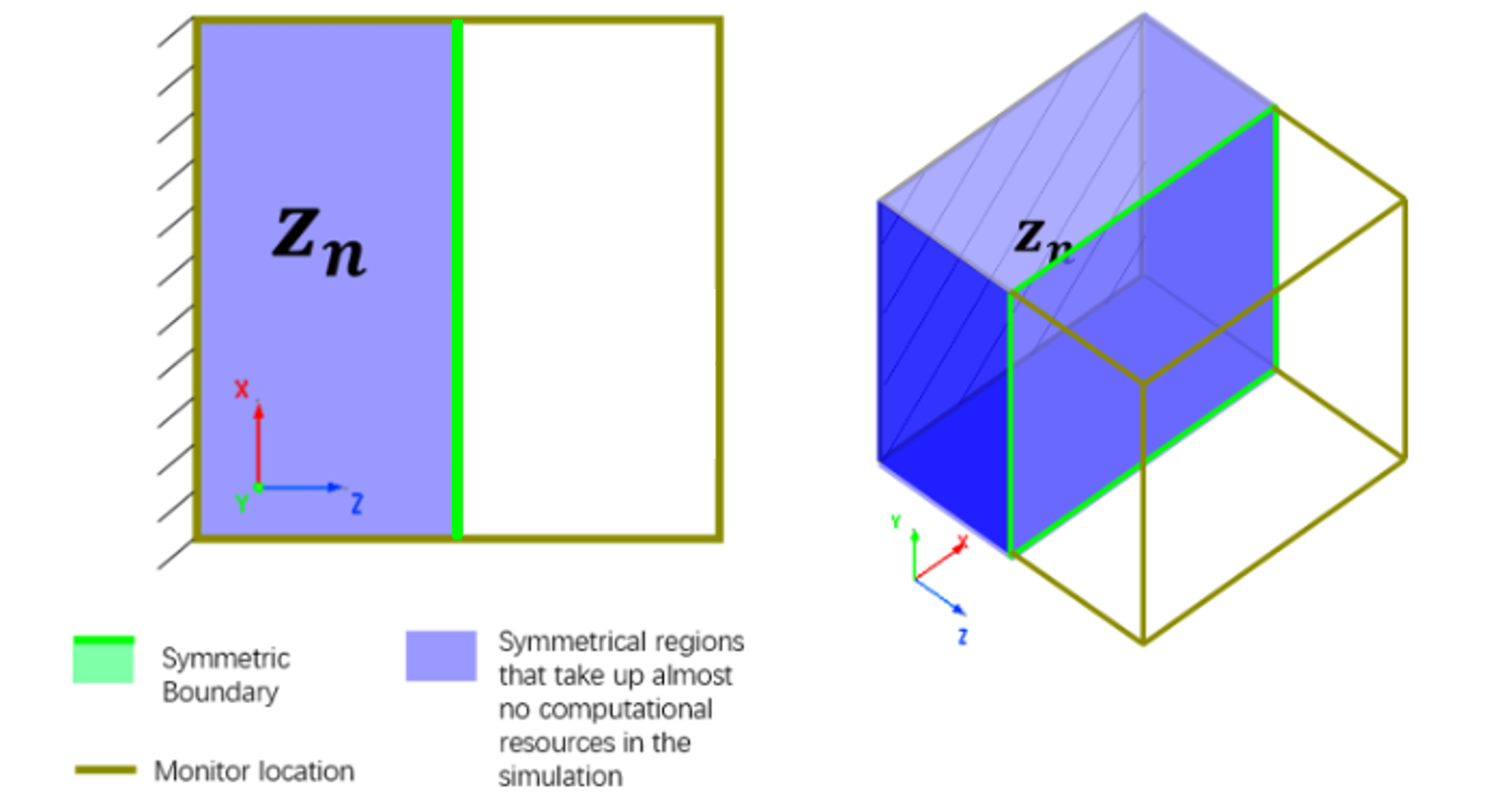
For periodic boundaries, simulation projects that satisfy the symmetry conditions are allowed to use symmetric/anti-symmetric boundary as equivalent replacements to minimize the simulation calculation loads.