This section is an introduction to 2.5D effective index theory and the unique settings for 2.5D finite difference time domain (FDTD) and 2.5D finite difference frequency domain (FDFD).

2.5D Finite Difference Time Domain (FDTD) Solver

The 2.5D finite difference time domain (FDTD) solver is integrated into the FDTD solution. When the user selects 2.5D in the Dimension and Polarization tab of FDTD, it will be automatically enabled. The 2.5D settings tab will appear, where the user can make relevant settings. The 2.5D FDTD solver can be used in large-scale 3D devices, where the structure and material remain completely constant or only have a few discrete variations in the height direction. The dimensions of such devices can sometimes reach hundreds of micrometers, which would require a significant amount of memory and computational resources in the 3D FDTD simulation. Currently, the 2.5D FDTD solver performs exceptionally well in the field of planar waveguides. By collapsing the third dimension and refining the mesh to run a 2D FDTD simulation, it will greatly speed up simulations and accelerate the device design.

Principles and Methods of Calculation

The fundamental principle of the 2.5D FDTD solver is to simplify a complex 3D problem into a 2D problem by generating new 2D materials to replace the original 3D structures using the effective indices method. This theoretical approach is based on the variational effective index approximation proposed by Hammer and Ivanova ^[1]. It solves for the effective refractive index in the vertical height direction, and calculates the 2D effective indices to perform 2D FDTD simulation. Additionally, during broadband simulations, the effective refractive index varies at different frequencies. The generated 2D effective materials will exhibit dispersion characteristics, with some coming from the original material and others from shape compression. The specific method is as follows:

$\varepsilon_{eff}^{TE}(x,y,\omega)=(\cfrac{\beta_r}{k})^2+\cfrac{\int_y(\varepsilon(x,y,z)-\varepsilon_r(y,\omega)\chi_r^2)dy}{\int_y\chi_r^2dy}$

$\varepsilon_{eff}^{TM}(x,y,\omega)=(\cfrac{\beta_r}{k})^2\cdot\cfrac{ \int_y\cfrac{1}{\varepsilon_r(y,\omega)}\chi_r^2dy}{\int_y\cfrac{1}{\varepsilon(x,y,z)}\chi_r^2dy}+\cfrac{\int_y(\cfrac{1}{\varepsilon_r(y,\omega)}-\cfrac{1}{\varepsilon(x,y,z)})(\partial_y\chi_r)^2dy}{k^2\int_y\cfrac{1}{\varepsilon(x,y,z)}\chi_r^2dy}$

where $\beta_r,\varepsilon_r,$ and $\chi_r$ denote the one-dimensional propagation constants, relative permittivity, and mode distribution in the vertical height direction. This method assumes to ignore the coupling between different waveguide slab modes. In this case, the waveguide will only support mutually perpendicular TE and TM modes, thereby approximating it as a 2D simulation.
The process of the 2.5D FDTD solver is as follows:

The following will provide a detailed explanation of several steps in the 2.5D solver.

• For step 1, the user needs to set it in the 2.5D settings section, refer to the Slab position section on this page. Users should be cautious when choosing this position, as it will directly affect whether the effective index for mode solving is correct. The height of this position should cover as much as possible all the structures that need to be studied;
• For step 2, users can set whether the effective material for 3D compression to 2D is a narrowband dielectric material or a broadband dispersive material, as well as the number of solving modes. For related settings, please refer to the Waveguide dispersion (bandwidth) and Slab mode sections on this page. The modeling results will be displayed on the Wave shape page. Selecting different modes that they want to study will obtain different effective materials. When obtaining the effective material for single frequency or narrowband, please select Narrow Bandwidth (Ignore Waveguide Dispersion). When the simulated project is sensitive to dispersion or the simulated material exhibits significant dispersion, please check Broad Bandwidth to calculate the 2D effective material. Then, it will be required to input the value of Number of samples (wavelength points), which is used for material fitting. The more points there are, the more accurate the fitting of effective 2D dispersion material will be;
• For step 3, the process of establishing 2D effective indices will be automatically performed by the software, which will create a proprietary material library for 2.5D materials. Users can click on Material to select Open check material library, where they can view the effective index at Slab position and Test position.

In addition to the above, users should note that in 2.5D solver, the 3D structure will be collapsed into a 2D plane, and the height option (y-direction by default in the software) in the FDTD solver and monitor will be meaningless. The results will be consistent when the monitor is placed at any height.

Application Examples

The following show how to build a 2.5D simulation using the Silicon Based Double Straight Waveguide Microring Resonator case. The resonant cavity is composed of silicon material, with a substrate of silicon dioxide.
After selecting 2.5D, the following 2.5D settings page will appear, which allows users to select the position of the slab mode and broadband settings.

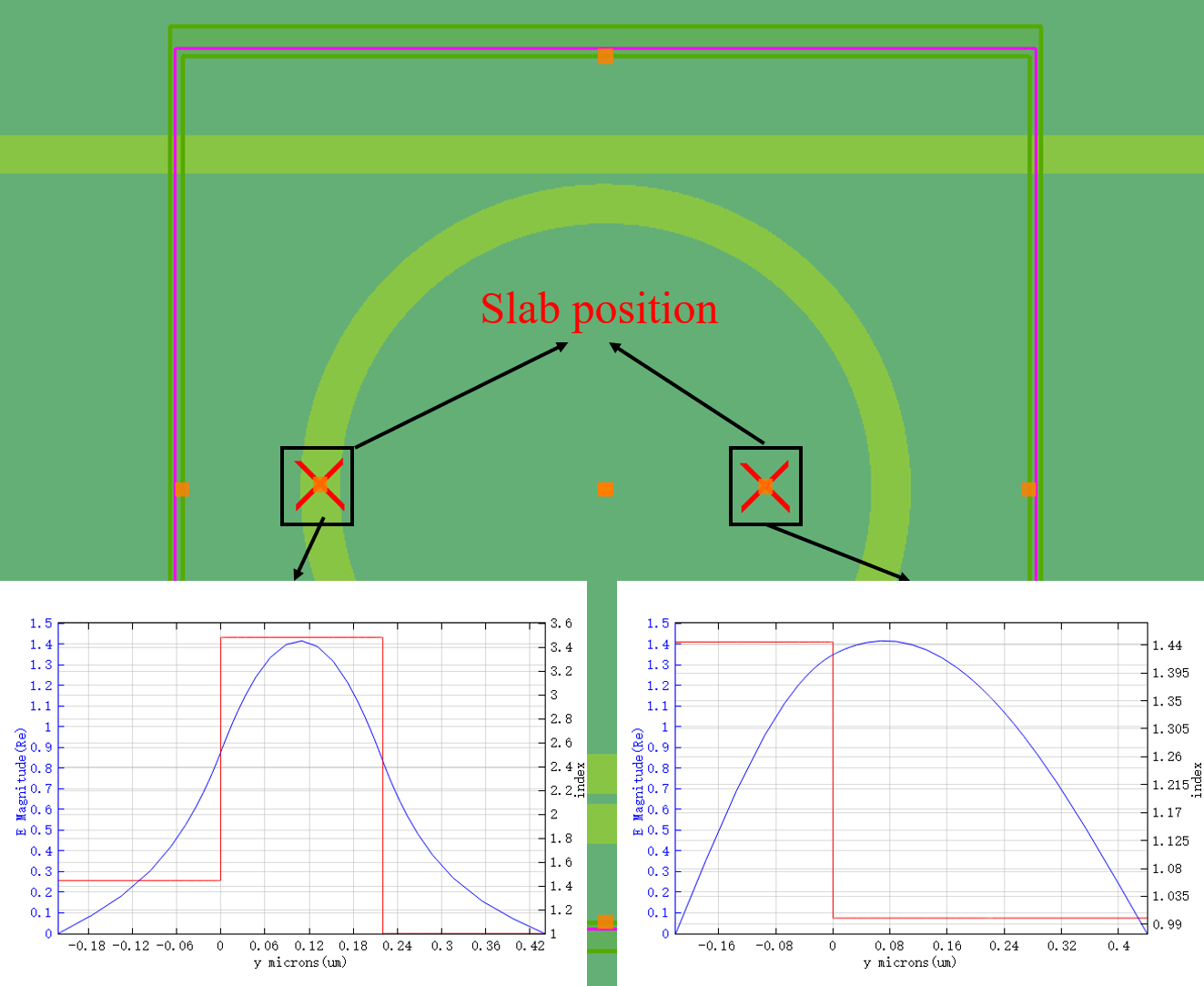
Since the incident light propagates mainly in the silicon circular resonance cavity, the Slab position should be chosen to calculate the location of the resonance cavity. The figure below shows the results of the fundamental mode at different positions.

In this case, it is necessary to obtain the transmission efficiency at multiple frequency points. Therefore, choosing broadband simulation and selecting the fundamental mode for simulation is recommended. Users can see the changes of the effective index of the core position and test position calculated in different options in the Open check material library.

2.5D Finite Difference Frequency Domain (FDFD) Solver

The 2.5D finite difference frequency domain (FDFD) solver is still integrated in the FDFD solution. The principle and method of compressing dimensions are the same as those of the 2.5D FDTD solver. After setting up the 2.5D settings page, other settings are universal. There is no need to elaborate further, you can proceed directly to run the simulation.

2.5D Solver Setting

Waveguide Dispersion

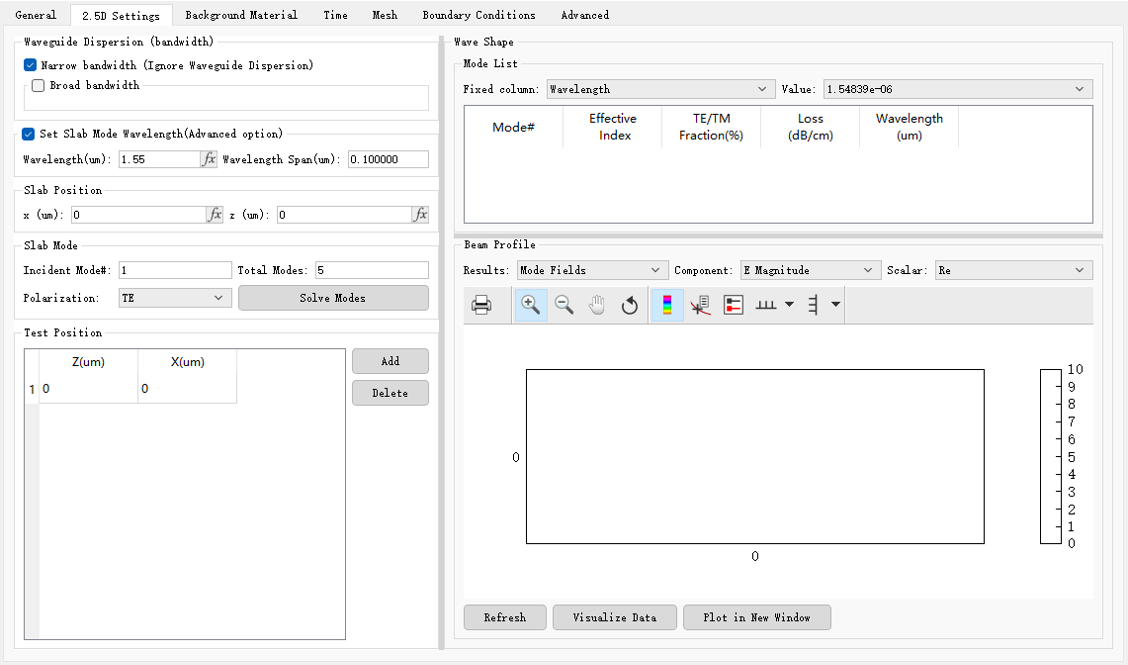
The Waveguide dispersion (bandwidth) tab is used to set the bandwidth of an equivalent 2D material.

Name	Description
Narrow bandwidth (ignore waveguide dispersion)	This option is suitable for single-frequency simulations or simulations with a very narrow bandwidth. The material properties are only taken at the center frequency of the simulation bandwidth.
Broad bandwidth	Check this option to enable broadband simulation, which requires to set the parameters for material fitting.
Number of samples (wavelength points)	When Broad bandwidth is checked, enable this option to set the number of wavelength points used for material fitting.
Tolerance(RMSE)	When Broad bandwidth is checked, enable this option to set the maximum tolerance allowed between the fitting model and the material sample points.
Max coefficients	When Broad bandwidth is checked, enable this option to set the highest order allowed for the polynomial of the fitting model.

Set Slab Mode Wavelength (Advanced Option)

The Set slab mode wavelength (advanced option) tab is used to specify the wavelength used in the mode solving for the slab waveguide. Check to enable this option.

Position of Slab Waveguide

The Slab position tab is used to set the (x, z) coordinates of the center of the slab waveguide during the mode solving process.

Slab Mode

Name	Description
Incident mode#	The number of the incident mode. After the mode solving is completed, the series number of the incident mode is displayed in the mode list.
Total modes	The total number of modes, i.e., the maximum number of modes returned in the mode list.
Polarization	Select the TE/TM polarization from the drop-down list.
Solve modes	Solve modes.

Test Position

The Test position tab is used to create the (z, x) coordinates of a material test point.

Name	Description
Add	Add the coordinates of a test point.
Delete	Delete the coordinates of a test point.

Wave Shape

The Wave shape tab includes a mode list and field components.

• Mode list

The Mode list displays the mode information obtained from mode solving.

Name	Description
Mode#	The serial number of a mode.
Effective index	The effective refractive index of a mode.
TE/TM fraction(%)	The ratio between TE and TM energy distribution in a mode.
Loss	The transmission loss of a mode, i.e., the energy attenuation of optical signals in waveguide devices due to factors such as absorption, scattering, etc.
Wavelength	The wavelength corresponding to a mode.

• Component

The Component tab is used to select field components for the Plot window and perform operations on the selected field components.

Name	Description
Component	Select field components for the Plot window: TE: Ex, Hy, Hz; TM: Ey, Ez, Hx.
Scalar	Abs: the modulus of the selected field component; Re: the real part of the selected field component; Im: the imaginary part of the selected field component; Phase: the argument of the selected field component.

---

1. Hammer M , Ivanova O V .Effective index approximations of photonic crystal slabs: a 2-to-1-D assessment[J].Optical and Quantum Electronics, 2009, 41(4):267-283. ↩︎