/

基础数学

Basic mathElementary math functionsVector operation

This section describes the elementary math functions.

abs

Description
Computes the absolute value of real number or the modulus of complex number.
Used in FDTD and FDE.

Syntax

Code	Function
`m = abs(num);`	Computes the absolute value of real number or the modulus of complex number.

Example

z = 3 + 4i;

m = abs(z)

Result:

m =
             5

See also
real

angle

Description
Returns the angle of a complex number or each complex number of matrix in radians.
Used in FDTD and FDE.

Syntax

Code	Function
`angle(comp_num);`	Returns the angle of the complex number comp_num in radians.
`angle(comp_matrix);`	Returns the angle of each complex number in matrix comp_matrix in radians.

See also
real

real

Description
Returns the real part of the input.
Used in FDTD and FDE.

Syntax

Code	Function
`out = real(A);`	Returns the real part of the input. If the argument is a matrix, then the real operation is performed on an element-by-element basis.

Example

X = [1+2j, 1+3j; 2, 1-2j ]

out = real(X)

Result:

X =
              1 +           2i              1 +           3i
              2 +           0i              1 -           2i
out =
             1             1
             2             1

See also
conj, imag

imag

Description
Returns the imaginary part of the input.
Used in FDTD and FDE.

Syntax

Code	Function
`out = imag(A);`	Returns the imaginary part of the input. If the argument is a matrix then the imag operation is performed on an element-by-element basis.

Example

X = [1+2j, 1+3j; 2, 1-2j ]

out = imag(X)

Result:

X =
              1 +           2i              1 +           3i
              2 +           0i              1 -           2i
out =
             2             3
             0            -2

See also
real

conj

Description
Complex conjugate.
Used in FDTD and FDE.

Syntax

Code	Function
`out = conj ( A );`	Returns the complex conjugate of its input argument. For matrix argument, the complex conjugate operation is performed element by element.

Example

b = [1+2j, 3+4j; 5, 6-7j]

out = conj(b)

Result:

b =
              1 +           2i              3 +           4i
              5 +           0i              6 -           7i
out =
              1 -           2i              3 -           4i
              5 +          -0i              6 +           7i

See also
imag

pow

Description
Calculates the power of a specified number.
Used in FDTD and FDE.

Syntax

Code	Function
`pow(base, exponent);`	Calculates the power of the input number base. The second input number is exponent.

Example

pow(2,3)

Result:

val =
             8

See also
sqrt

dot

Description
Calculates the dot product of the input vectors or matrices.
Used in FDTD and FDE.

Syntax

Code	Function
`out = dot(A, B)`	A, B must be 3 * n matrices. Calculates dot product between column vector A(:,i) and the corresponding column vector B(:,i).

Example

A = [1, 0; 0, 1; 0 , 0]
B = [1, 0; 0, 2; 0 , 0]

dot(A, B)

Result:

A =
             1             0
             0             1
             0             0
B =
             1             0
             0             2
             0             0
val =
             1             2

See also
cross

cross

Description
Computes the vector cross product.
Used in FDTD and FDE.

Syntax

Code	Function
`out = cross(A, B);`	Computes the vector cross product of vector A and B(two 3-by-1 matrices). If A and B are matrices, they must be 3 * n matrices, the `cross` function will calculate the cross product between A(:, m) and B(:, m).

See also
dot

cumprod

Description
Computes the running or cumulative product of the input.
Used in FDTD and FDE.

Syntax

Code	Function
`out = cumprod ( A );`	Computes the running or cumulative product of the input A. If the input is a rectangular matrix, then the cumulative product operation is performed over each column of the matrix respectively.

Example

a = 1:4 
b = cumprod (a)

Result:

a =
             1             2             3             4
b =
             1             2             6            24

See also
cumsum

cumsum

Description
Cumulative sum.
Used in FDTD and FDE.

Syntax

Code	Function
`out = cumsum ( A );`	Computes the running or cumulative sum of a vector or matrix. The return object is a matrix the same size as input A. If A is a rectangular matrix, then the cumulative sum operation is performed over each column of the matrix respectively.

Example


b = [1,2,3;4,5,6;7,8,9]
b_cusum = cumsum(b)

Result:

b =
             1             2             3
             4             5             6
             7             8             9
b_cusum =
             1             2             3
             5             7             9
            12            15            18

See also
cumprod, prod, sum

all

Description
Checks if all elements are non-zero.
Used in FDTD and FDE.

Syntax

Code	Function
`out = all( A);`	When A is a vector (row or column), returns 1 if all elements of A are non-zeros, otherwise returns 0. When A is a matrix, `all` function will operate on each column of A respectively, returning a row-vector of ones and zeros.

Example

A = [1, 2, 3; 4, 0, 5];

out = all(A)

Result:

out =
             1             0             1

See also
any

any

Description
Checks if any elements are non-zero.
Used in FDTD and FDE.

Syntax

Code	Function
`out = any(A);`	When A is a vector (row or column), returns 0 if any element of A is zero, otherwise returns 1. When A is a matrix, `any` function will operate on each column of A respectively, returning a row-vector of ones and zeros.

Example

A = [1, 2, 0; 4, 0, 0];

out = any(A)

Result:

out =
             1             1             0

See also
all

iscolumn

Description
Determines whether a vector is a column vector.
Used in FDTD and FDE.

Syntax

Code	Function
`out = iscolumn(a);`	Determines whether a vector is a column vector. If the input a is a column vector, returns 1.

See also
isrow

isrow

Description
Determines whether a vector is a row vector.
Used in FDTD and FDE.

Syntax

Code	Function
`out = isrow(a);`	Determines whether a vector is a row vector. If the input a is a row vector, returns 1.

See also
iscolumn

ceil

Description
Returns the smallest integer not less than the input argument.
Used in FDTD and FDE.

Syntax

Code	Function
`out = ceil ( a );`	Returns the smallest integer not less than the input argument. If the argument is a matrix, then the ceil operation is performed on an element-by-element basis.

Example

b = rand(2, 3).*10

out = ceil( b )

Result:

b =
     7.4853313     6.4248842   0.889701694
    3.85106683    7.78148055    7.96419024
out =
             8             7             1
             4             8             8

fix

Description
Rounds each element of matrix X to the nearest integer towards zero.
Used in FDTD and FDE.

Syntax

Code	Function
`out = fix(X);`	Rounds each element of matrix X to the nearest integer towards zero.

Example

X = [-1.5, 2.3; 1.5 ,0]

out = fix(X)

Result:

X =
          -1.5           2.3
           1.5             0
out =
            -1             2
             1             0

See also
ceil, floor, round, sign, abs

floor

Description
Returns the largest integer not greater than the argument. If the argument is a matrix, then the floor operation is performed on an element-by-element basis.
Used in FDTD and FDE.

Syntax

Code	Function
`out = floor(X);`	Returns the largest integer not greater than the argument. If the argument is a matrix, then the floor operation is performed on an element-by-element basis.

Example

X = [-1.5, 2.3; 1.5 ,0]

out = floor(X)

Result:

X =
          -1.5           2.3
           1.5             0
out =
            -2             2
             1             0

See also
ceil

round

Description
Returns the nearest integer value to its floating point input X as a double-precision floating point number.
Used in FDTD and FDE.

Syntax

Code	Function
`out = round(X);`	Returns the nearest integer value to its floating point input X as a double-precision floating point number. The returned value is rounded according to the currently set machine rounding mode. If round-to-nearest is set and the difference between the function argument and the rounded result is exactly 0.5, then the result will be rounded to the nearest even integer.

Example

A = rand(2, 3).*10

B = round(A)

Result:

A =
    2.07460493    9.58588481    5.36877036
    0.66318281    7.68718481    6.99025512
B =
             2            10             5
             1             8             7

See also
floor, ceil

int

Description
Converts the input to integer.
Used in FDTD and FDE.

Syntax

Code	Function
`out = int(X);`	Converts the input to integer. If the argument is a matrix then the int operation is performed on an element-by-element basis.

Example

b = 3.14159;
b_int = int(b)

Result :

b_int =
             3

See also
ceil, floor

max

Description
Returns the maximum value(s).
Used in FDTD and FDE.

Syntax

Code	Function
`out = max(A);`	Returns the maximum value(s) contained in the matrix. If the input A is a vector, returns the maximum value of it. If the input A is a matrix, returns a row-vector containing the maximum values from each column of A.
`out = max(A, B);`	Returns a matrix the same size as matrix A. The matrices A and B must be the same size. The output matrix out contains the larger of the corresponding elements in A and B.

Note :
When matrix elements are complex the absolute value is used for comparison purposes.

Example

b = [1, 3, -1; 3, 0.5, 6]
out = max(b)

Result:

b =
             1             3            -1
             3           0.5             6
out =
             3             3             6

See also
maxi, min, mini

maxi

Description
Returns the index of the maximum value.
Used in FDTD and FDE.

Syntax

Code	Function
`out = maxi( A );`	Returns the index of the maximum value. If A is a vector, returns the index of the largest value. If A is a M * N matrix, returns a row-vector of the row indices of the largest column values of A.

See also
max, min, mini

min

Description
Returns the minimum value(s) contained in the matrix.
Used in FDTD and FDE.

Syntax

Code	Function
`out = min(A);`	Returns the minimum value(s) contained in the matrix. If the input A is a vector, returns the smallest value of it. If the input A is a matrix, returns a row-vector containing the minimum values from each column of A.
`out = min(A, B);`	Returns a matrix the same size as matrix A. The matrices A and B must be the same size. The output matrix out contains the smaller of the corresponding elements in A and B.

Note:
When matrix elements are complex the absolute value is used for comparison purposes.

Example

b = [1, 3, -1; 3, 0.5, 6]
out = min(b)

Result:

b =
             1             3            -1
             3           0.5             6
out =
             1           0.5            -1

See also
mini, max, maxi

mini

Description
Returns the index of the minimum value.
Used in FDTD and FDE.

Syntax

Code	Function
`out = mini( A );`	Returns the index of the minimum value. If A is a vector, returns the index of the minimum value. If A is a M * N matrix, returns a row-vector of the row indices of the minimum column values of A.

See also
max, maxi, min

findpeaks

Description
Finds the peaks from the spectrum or others.
Used in FDTD and FDE.

Syntax

Code	Function
`[val, ind] = findpeaks(D, num);`	Returns the indexes of local maxima(peaks) ind and values of local maxima(peaks) val of the input vector or matrix D. The parameter num is the number of local maxima(peaks) to be returned. If the number of local maxima that can actually be found is less than the value of num , then the `findpeaks` function will return the local maxima that can actually be found and throw a warning.

Example

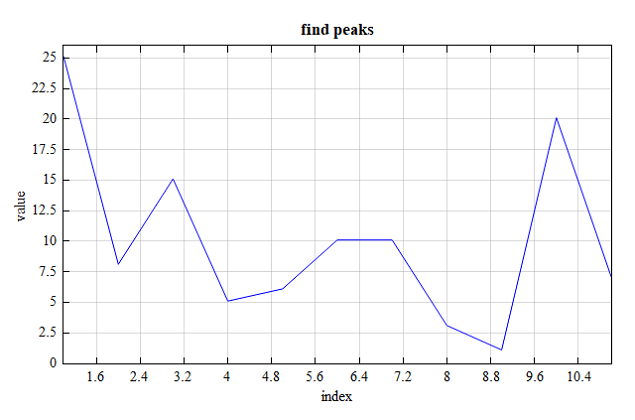
closeall;
clearall;

# findpeaks() can find peaks of a vector
vector = [25.1,8.1,15.1,5.1,6.1,10.1,10.1,3.1,1.1,20.1,7.1];  # signal
[peaks_val,peaks_ind] = findpeaks(vector, 5);  # return a list about val and ind

figure();
plot(1:length(vector), vector,'b');   
xlabel('index');
ylabel('value');
title('find peaks');

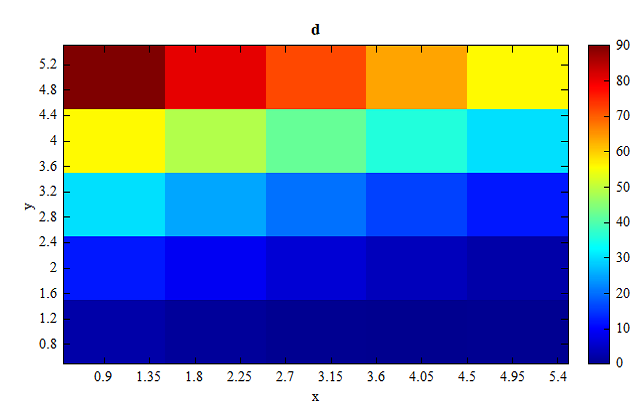
# findpeaks() also can find peaks of a matrix
x = [1, 2, 3, 4, 5];
y = [1, 2, 3, 4, 5];
d = zeros(length(x),length(y));
for (i = 1:length(x))     
	for(j = 1:length(y))             
		d(i,j) =(2*x(i)-0.5*y(j)).^2;    
	end 
end
[peaks_val2,peaks_ind2] = findpeaks(d, 5);

figure(); 
image(x,y,d);
xlabel('x');
ylabel('y');

Result:

> peaks_ind
peaks_ind =
            10             3             6
> peaks_val
peaks_val =
          20.1          15.1          10.1
> peaks_ind2
peaks_ind2 =
             5            10            15            20
> peaks_val2
peaks_val2 =
         90.25            81         72.25            64

The figures show the output of the example code:
vector:
/findpeaks_example_vector.png

matrix d:

sort

Description
Sorts array elements.
Used in FDTD and FDE.

Syntax

Code Function

[val,ind] = sort(A) If A is a vector (either row or column), then val and ind are sorted values and indices. If A is a matrix (m > 2), the sort operation will be performed on each column of A respectively, then val is the sorted columns of A, and ind is the sorted indices of A. Numerical matrices are sorted in ascending numerical value. Complex matrices are sorted by absolute value. String matrices are sorted alphabetically (using strcmp()).

Code	Function
`[val,ind] = sort(A)`	If A is a vector (either row or column), then val and ind are sorted values and indices. If A is a matrix (m > 2), the sort operation will be performed on each column of A respectively, then val is the sorted columns of A, and ind is the sorted indices of A. Numerical matrices are sorted in ascending numerical value. Complex matrices are sorted by absolute value. String matrices are sorted alphabetically (using `strcmp()`).

Example

  m=[2,54,78,1,34,78,99,55];
  [val,ind] = sort(m);

Result:

 val =
             1             2            34            54            55            78            78            99

ind =
             4             1             5             2             8             6             3             7

sort2

Description
Rearranges matrix according to the given index.
Used in FDTD and FDE.

Syntax

Code	Function
`[fxy2,xs,ys] = sort2(fyx, y, x);`	Rearranges matrix according to the given index.

Example

aa = [1,2,3;4,5,6;3,1,4]

sort2( aa, [1,2,3],[1,3,2] )

Result:

aa =
             1             2             3
             4             5             6
             3             1             4
val =
             1             2             3
             3             1             4
             4             5             6

See also
sort

flip

Description
Reverses the order of elements in designated vector or matrix.
Used in FDTD and FDE.

Syntax

Code	Function
`flip(V)`	Reverses the order of elements in designated vector V. If the input V is a matrix, flip operation will be performed on each column of matrix V respectively.

Example

V = [1, 3, 5, 7, 3]

R = flip(V)

Result:

V =
             1             3             5             7             3
R =
             3             7             5             3             1

See also
sort, sort2

inf

Description
Returns a scalar whose value is infinity, according to IEEE-754. Unlike NaN, inf == inf should return TRUE (1).
Used in FDTD and FDE.

Syntax

Code	Function
`out = inf;`	Returns a scalar whose value is infinity.

Example

inf_1 = inf;
inf_2 = inf;

inf_1 == inf_2

Result:

val =
             1

See also
nan

nan

Description
Returns a NaN (Not a Number) according to IEEE-754. One way to determine if a variable contains a NaN is to test it against itself. NaN == NaN should always return FALSE (0).
Used in FDTD and FDE.

Syntax

Code	Function
`out = nan;`	Returns a `NaN` (Not a Number).

Example

out = nan;
out_2 = nan;

out == out_2

Result:

val =
             0

See also
inf

mod

Description
Returns the floating point remainder of the division of A by B.
Used in FDTD and FDE.

mod(A, B) returns A if B is zero or A/B would overflow, otherwise returns the number F with the same sign as B, such that A = k * B + F for some integer k, and |F| < |B|.

When the arguments for mod are two matrices, then an element-by-element mod operation is performed. mod works on complex number also.

mod(x,y) is equivalent to:

mod(x,y) = x - y * floor(x/y)

The mod function follows the convention that mod(x,0) returns x.

Syntax

Code	Function
`out = mod(A, B);`	Returns the floating point remainder of the division of A by B.

Example

x = 10;
y = 3;

z = mod(x, y)

Result:

z =
             1

See also
rem

prod

Description
Computes the product of the elements of A (if A is a vector). If A is a matrix, returns a row vector containing the products of each column.
Used in FDTD and FDE.

Syntax

Code	Function
`out = prod ( A );`	Computes the product of the elements of A (if A is a vector). If A is a matrix, returns a row vector containing the products of each column.

Example

A = [1, 2; 3, 6]

b = prod(A)

Result:

A =
             1             2
             3             6
b =
             3            12

See also
mod, cumprod

rem

Description
Calculates the remainder of A / B.
Used in FDTD and FDE.

Note:
The mod( A, B ) is equivalent to rem( A, B). mod is a built-in function, and is much faster when operating on matrices. rem is provided mostly for MATLAB compatibility.

Syntax

Code	Function
`out = rem(A, B);`	Calculates the remainder of A / B.

Example

x = 10;
y = 3;

z = rem(x, y)

Result:

z =
             1

See also
mod

sign

Description
Returns the sign of A. For a complex scalar, sign returns: A ./ abs (A) .
The sign function performs its operation on real and complex matrices in an element-by-element fashion.

Used in FDTD and FDE.

Syntax

Code	Function
`out = sign ( A );`	Returns the sign of A.

Example

z = 3 + 4j;

out = sign(z)

Result:

out =
            0.6 +         0.8i

acos

Description
Computes the arc-cosine.
Used in FDTD and FDE.

The trigonometric functions are scalar functions. The return value is the result of the trigonometric operation performed on the input, element by element.

All the trigonometric functions use the C language math library functions, so details about the ranges and error conditions can be found by examining the appropriate manual pages on your system.

Syntax

Code	Function
`out = acos( A );`	Computes the arc-cosine.

Example

out = acos(0.5)

Result:

out =
    1.04719755

See also
asin

asin

Description
Computes the arc-sin.
Used in FDTD and FDE.

The trigonometric functions use the C language math library functions, so details about the ranges and error conditions can be found by examining the appropriate manual pages on your system.

Syntax

Code	Function
`out = asin(A);`	Computes the arc-sin.

Example

out = asin(0.5)

Result:

out =
   0.523598776

See also
acos

atan

Description
Computes the arc-tangent.
Used in FDTD and FDE.

The trigonometric functions use the C language math library functions, so details about the ranges and error conditions can be found by examining the appropriate manual pages on your system.

Syntax

Code	Function
`out = atan( A );`	Computes the arc-tangent.

Example

out = atan(0.5)

Result:

out =
   0.463647609

See also
asin

atan2

Description
Computes the arc-tangent.
Used in FDTD and FDE.

The atan2 function takes two arguments, which are the y, and x values used to form the tangent. All the trigonometric functions use the C language math library functions, so details about the ranges and error conditions can be found by examining the appropriate manual pages on your system.

atan2 does not operate on complex arguments.

Syntax

Code	Function
`out = atan2( y , x );`	Computes the arc-tangent of y/x.

Example

y = 1;
x = 2;
at = atan2(y, x)

Result:

at =
   0.463647609

See also
atan

cos

Description
Computes the cosine.
Used in FDTD and FDE.

The trigonometric functions are scalar functions. The return value is the result of the trigonometric operation performed on the input, element by element.

All the trigonometric functions use the C language math library functions, so details about the ranges and error conditions can be found by examining the appropriate manual pages on your system.

Syntax

Code	Function
`out = cos( A );`	Computes the cosine.

See also
sin

sin

Description
Computes the sine.
Used in FDTD and FDE.

All the trigonometric functions use the C language math library functions, so details about the ranges and error conditions can be found by examining the appropriate manual pages on your system.

Syntax

Code	Function
`out = sin( A );`	Computes the sine.

See also
cos

tan

Description
Computes the tangent.
Used in FDTD and FDE.

All the trigonometric functions use the C language math library functions, so details about the ranges and error conditions can be found by examining the appropriate manual pages on your system.

Syntax

Code	Function
`out = tan( A );`	Computes the tangent.

See also
sin, cos

acosd

Description
Computes the arc-cosine, the output argument's unit is degree.
Used in FDTD and FDE.

The trigonometric functions are scalar functions. The return value is the result of the trigonometric operation performed on the input, element by element.

All the trigonometric functions use the C language math library functions, so details about the ranges and error conditions can be found by examining the appropriate manual pages on your system.

Syntax

Code	Function
`out = acosd( A );`	Computes the arc-cosine, the output argument's unit is degree.

See also
asind

asind

Description
Computes the arc-sin, the output argument's unit is degree.
Used in FDTD and FDE.

The trigonometric functions use the C language math library functions, so details about the ranges and error conditions can be found by examining the appropriate manual pages on your system.

Syntax

Code	Function
`out = asind(A);`	Computes the arc-sin, the output argument's unit is degree.

See also
atand

atand

Description
Computes the arc-tangent, the output argument's unit is degree.
Used in FDTD and FDE.

The trigonometric functions use the C language math library functions, so details about the ranges and error conditions can be found by examining the appropriate manual pages on your system.

Syntax

Code	Function
`out = atand( A );`	Computes the arc-tangent, the output argument's unit is degree.

See also
atan2d

atan2d

Description
Computes the arc-tangent, the output argument's unit is degree.
Used in FDTD and FDE.

atan2 takes two arguments, which are the y, and x values used to form the tangent. All the trigonometric functions use the C language math library functions, so details about the ranges and error conditions can be found by examining the appropriate manual pages on your system.

atan2 does not operate on complex arguments.

Syntax

Code	Function
`out = atan2d( y , x );`	Computes the arc-tangent of y / x , the output argument's unit is degree.

See also
cosd

cosd

Description
Computes the cosine, the input argument's unit is degree.
Used in FDTD and FDE.

The trigonometric functions are scalar functions. The return value is the result of the trigonometric operation performed on the input, element by element.

All the trigonometric functions use the C language math library functions, so details about the ranges and error conditions can be found by examining the appropriate manual pages on your system.

Syntax

Code	Function
`out = cosd( A );`	Computes the cosine, the input argument's unit is degree.

See also
sind

sind

Description
Computes the sine, the input argument's unit is degree.
Used in FDTD and FDE.

All the trigonometric functions use the C language math library functions, so details about the ranges and error conditions can be found by examining the appropriate manual pages on your system.

Syntax

Code	Function
`out = sind( A );`	Computes the sine, the input argument's unit is degree.

See also
tand

tand

Description
Computes the tangent, the input argument's unit is degree.
Used in FDTD and FDE.

Syntax

Code	Function
`out = tand( A );`	Computes the tangent of an input argument in degrees. The function supports scalar and matrix arguments.

See also
sind, cosd

log

Description
Returns the natural logarithm of its input parameter.
Used in FDTD and FDE.

Syntax

Code	Function
`out = log( A );`	Returns the natural logarithm of its input parameter. If the input parameter is a vector or matrix, an element-by-element log operation is performed.

See also
log10

log10

Description
Returns the base-10 logarithm of its input parameter.
Used in FDTD and FDE.

Syntax

Code	Function
`out = log10( A );`	Returns the base-10 logarithm of its input parameter. If the input parameter is a matrix, an element-by-element log10 operation is performed.

Note:The log10 function is not implemented yet for COMPLEX data.

See also
log

exp

Description
Returns the value of e (the base of natural logarithms) raised to the power of X.
Used in FDTD and FDE.

Syntax

Code	Function
`out = exp(A);`	Returns the value of e (the base of natural logarithms) raised to the power of X. If the argument to `exp` is a matrix then an element-by-element operation is performed.

See also
fexp

frexp

Description
Converts floating-point number to fractional and integral components.
Used in FDTD and FDE.

frexp returns a struct containing f (0.5 <= abs(f) <= 1) and exponent e, the input A can be represented:

A = f * 2^{e}

If A is zero, then both e and f are zero.

frexp operates on REAL matrices of any dimension.

Syntax

Code	Function
`out = frexp( A );`	Returns a struct with elements f and e. `frexp` splits A into a normalized fraction which is returned in f and has the absolute value in interval [0.5, 1.0], and a power of 2 which is returned in e.

Example

out = frexp(5)

out.f*2.^out.e

Result:

out =
  struct with fields:
    e: 3
    f: 0.625
val =
             5

See also
ldexp

ldexp

Description
Multiplies floating point number by integral power of 2.
Used in FDTD and FDE.

ldexp returns a numeric matrix which contains the value(s) resulting from the operation:

X * 2^{EXP}

The dimensions of X and EXP must be the same. Optionally, EXP can be a scalar, independent of the size of X.

Syntax

Code	Function
`out = ldexp( X , EXP );`	Multiplies floating point number X by integral ( EXP ) power of 2.

See also
frexp

sqrt

Description
Returns the square-root of its input parameter.
Used in FDTD and FDE.

Syntax

Code	Function
`out = sqrt( A );`	Returns the square-root of its input parameter. If the input parameter is a matrix, then an element-by-element square-root operation is performed. The `sqrt(-1)` will produce 1i.

See also
pow

sum

Description
Sums the elements of a matrix.
Used in FDTD and FDE.

Syntax

Code	Function
`out = sum( A );`	Computes the sum of a matrix. If A is a vector, returns the sum of its elements. If A is a matrix, returns a row matrix containing the sums of each column of A.

union

Description
Returns a vector set that is the union of the two sets A and B.
Used in FDTD and FDE.

Syntax

Code	Function
`out = union(A, B);`	Returns a vector set that is the union of the two sets A and B.

complement

Description
Computes the complement of A in B.
Used in FDTD and FDE.

Syntax

Code	Function
`out = complement(A, B);`	Returns a vector set that is the complement of the two sets A and B.

See also
intersection, union

intersection

Description
Finds the intersection-set of the two vector sets A, B.
Used in FDTD and FDE.

Syntax

Code	Function
`ret = intersection( A , B );`	Finds the intersection-set of the two vector sets A, B.

See also
union, complement

compan

Description
Companion matrix.
Used in FDTD and FDE.

If the input P is a (n+1)-vector, compan( P ) is the n-by-n companion matrix whose first row is -P(2:n+1)/P(1).

Syntax

Code	Function
`out = compan( P );`	Returns the companion matrix of P .

See also
inv

cart2cyl

Description
Converts the Cartesian coordinate system to the cylindrical or polar coordinate system.
Used in FDTD and FDE.

Syntax

Code	Function
`[rho, theta] = cart2cyl(x, y);`	Converts the Cartesian coordinate (x, y) to the polar coordinate (rho, theta) . The inputs x, y can be numbers or vectors. When x, y are vectors, this function will convert (x(i), y(i)) to polar coordinate.
`[rho, theta] = cart2cyl(x, y, val);`	Converts the Cartesian coordinate (x, y) to the polar coordinate (rho, theta). val controls the direction of the conversion.
`[rho, theta, z] = cart2cyl(x, y, z);`	Converts the Cartesian coordinate (x, y, z) to the cylindrical coordinate (rho, theta, z). The inputs x, y, z can be numbers or vectors. When x, y, z are vectors, this function will convert (x(i), y(i), z(i)) to cylindrical coordinate.
`[rho, theta, z] = cart2cyl(x, y, z, val);`	Converts the Cartesian coordinate (x, y, z) to the cylindrical coordinate (rho, theta, z). val controls the direction of the conversion.

See also
cart2sph

cart2sph

Description
Converts the Cartesian coordinate system to the spherical coordinate system.
Used in FDTD and FDE.

Syntax

Code	Function
`[r, elevation, azimuth] = cart2sph(x, y, z);`	Converts the Cartesian coordinate (x, y, z) to the spherical coordinate (r, elevation, azimuth) . The inputs x, y, z can be numbers or vectors. When x, y, z are vectors, this function will convert (x(i), y(i), z(i)) to spherical coordinate.
`[r, elevation, azimuth] = cart2sph(x, y, z, val);`	Converts the Cartesian coordinate (x, y, z) to the spherical coordinate (r, elevation, azimuth). The inputs x, y, z can be numbers or vectors. val controls the direction of the conversion.

See also
cart2cyl

sph2cart

Description
Converts the spherical coordinate system to the Cartesian coordinate system.
Used in FDTD and FDE.

Syntax

Code	Function
`[x, y, z] = sph2cart(r, elevation, azimuth);`	Converts the spherical coordinate (r, elevation, azimuth) to the Cartesian coordinate (x, y, z). The inputs r, elevation, azimuth can be numbers or vectors. When r, elevation, azimuth are vectors, this function will convert (r(i), elevation(i), azimuth(i)) to Cartesian coordinate.

See also
cart2sph

cyl2sph

Description
Converts the cylindrical coordinate system to the spherical coordinate system.
Used in FDTD and FDE.

Syntax

Code	Function
`[r, elevation, azimuth] = cyl2sph(rho, theta, z);`	Converts the cylindrical coordinate (rho, theta, z) to the spherical coordinate (r, elevation, azimuth).
`[r, elevation, azimuth] = cyl2sph(rho, theta, z, val);`	Converts the cylindrical coordinate (rho, theta, z) to the spherical coordinate (r, elevation, azimuth). val controls the direction of the conversion.

See also
cart2cyl, cart2sph

linspace

Description
Generates a linearly spaced vector.
Used in FDTD and FDE.

Syntax

Code	Function
`ret = linspace ( s1 , s2 );`	Generates a vector containing 100 equally spaced points between s1 and s2 .
`ret = linspace ( s1, s2, n);`	Generates a vector containing n equally spaced points between s1 and s2 .

Example
Generates a vector containing 600 equally spaced points between $\pi$ and $2\pi$ .

L = linspace(pi, 2*pi, 600);

See also
logspace

logspace

Description
Generates a logarithmically spaced vector.
Used in FDTD and FDE.

Syntax

Code	Function
`out = logspace(L1, L2);`	Generates a vector containing 50 logarithmically spaced points between decades $10^{L1}$ and $10^{L2}$ .
`out = logspace(L1, L2, n);`	Generates a vector containing n logarithmically spaced points between decades $10^{L1}$ and $10^{L2}$ .

Example

L = logspace(1, 3, 1000);

See also
linspace

eye

Description
Creates an identity matrix with specified size.
Used in FDTD and FDE.

If the input is A, a matrix with two elements, then the 1st element of A determines the number of rows, and the 2nd element of A determines the number of columns of the new matrix.

The matrix input option exists so that:

eye( size( X ) )

will work.

Syntax

Code	Function
`eye(S1, S2)`	Creates a matrix whose elements are ones in the diagonal and zeros elsewhere with number of rows and columns specified by two scalars (S1 - rows, and S2 - columns). If S1 is equal to S2, the newly created matrix is an identity matrix.
`eye(A)`	Creates a matrix whose elements are ones in the diagonal and zeros elsewhere with number of rows and columns specified by a 1 * 2 matrix (A(1) - rows, and A(2) - columns).

See also
ones, zeros

ones

Description
Creates a matrix filled with ones. If the inputs are two scalars, then creates a matrix of 1s with dimensions N x M.
Used in FDTD and FDE.
If the input is a 2 element matrix, then creates a matrix with row and column dimensions equal to A[1] and A[2] respectively. This is useful when used in conjunction with size():

ones( size( X ) )

will return a matrix of ones the same size as X.

Syntax

Code	Function
`out = ones ( M , N )`	Creates a matrix of ones with number of rows and columns specified by two scalars (M - rows, and N - columns).
`out = ones ( A )`	Creates a matrix of ones with number of rows and columns specified by a 1 * 2 matrix (A(1) - rows, and A(2) - columns).

See also
zeros

zeros

Description
Returns a matrix with all zero elements.
Used in FDTD and FDE.

Syntax

Code	Function
`out = zeros ( M, N )`	Creates a matrix of zeros with number of rows and columns specified by two scalars (M - rows, and N - columns).
`out = zeros ( A )`	Creates a matrix of zeros with number of rows and columns specified by a 1 * 2 matrix (A(1) - rows, and A(2) - columns).

Examples

Z = zeros( 3 , 3 )
A = rand([2,4])
B = zeros( size(A) )
Size = size(B)

Result:

Z =
             0             0             0
             0             0             0
             0             0             0
A =
   0.740586579   0.759322286   0.324714601   0.651859522
   0.312950581   0.151108995   0.841534674   0.385818511
B =
             0             0             0             0
             0             0             0             0
Size =
             2             4

See also
ones

rand

Description
Random number generator.
Used in FDTD and FDE.

Syntax

Code	Function
`out = rand ( )`	Creates a random number.
`out = rand ( M, N )`	Creates a random matrix with M rows and N columns.
`out = rand ( DTYPE, ... )`	Changes the distribution used when generating random numbers.

If the first input parameter of rand() function is DTYPE , the value of DTYPE determines the subsequent parameters, details can be seen as following:

rand ( 'beta', a, b )
Sets the generator to return a random deviate from the beta distribution with parameters a and b. The density of the beta is

\frac{x^{(a-1)} * (1-x)^{(b-1)}} {B(a, b)} , for 0< x < 1

rand ( 'chi', DF )
Sets the generator to return a random deviate from the distribution of a chi-square with DF degrees of freedom random variable.
rand ( 'exp', AV )
Sets the generator to return a random deviate from an exponential distribution with mean AV.
rand ( 'f', DFN, DFD )
Sets the generator to return a random deviate from the F (variance ratio) distribution with DFN degrees of freedom in the numerator and DFD degrees of freedom in the denominator.
rand ( 'gamma', A, R )
Sets the generator to return a random deviate from the gamma distribution whose density is:

\frac{A^{R}}{\Gamma(R)} x^{R-1} e^{-Ax}

rand ( 'nchi', DF, XNONC )
Sets the generator to return a random deviate from the distribution of a noncentral chi-square with DF degrees of freedom and noncentrality parameter XNONC.
rand ( 'nf', DFN, DFD, XNONC )
Sets the generator to return a random deviate from the noncentral F (variance ratio) distribution with DFN degrees of freedom in the numerator, and DFD degrees of freedom in the denominator, and noncentrality parameter XNONC.
rand ( 'normal', AV, SD )
Sets the generator to return a random deviate from a normal distribution with mean, AV, and standard deviation, SD.
rand ( 'uniform', LOW, HIGH )
Sets the generator to return a uniform double between LOW and HIGH.
rand ( 'bin', N, P )
Returns a single random deviate from a binomial distribution whose number of trials is N and whose probability of an event in each trial is P.
rand ( 'poisson', AV )
Sets the generator to return a random deviate from a Poisson distribution with mean AV.
rand ( 'default' )
Resets the random number generator to the default generator, which generates a distributed random variable in the interval (0, 1). The interval endpoints are not returned.

Example

rand()

rand(1, 5)

rand('normal', 0, 1);

rand(1, 5)

Result:

val =
   0.999999702
val =
    0.97451961   0.647483885   0.333085597  0.0369445458   0.161711872
val =
  -0.382442355   0.173820451   0.490691006   0.389735132  -0.356648415

rand uses the RANLIB library, authored by B. W. Brown and J. Lovato under grant CA-16672 from the National Cancer Institute.

See also
srand

srand

Description
Sets the seed for the random number generator.
Used in FDTD and FDE.

Syntax

Code	Function
`srand()`	Sets the seed to the original value (the last value given to srand, or the default value, 1).
`srand(seed)`	Sets the random number seed to the designated value seed .
`srand("clock")`	Sets the seed based upon the machine clock value. This provides users a way of picking a unique seed each time.

Note:
srand uses the RANLIB subroutine SETALL.

Example

# Case 1: use different random number seed
# The matrix rand_num will be different from matrix rand_num_new.
srand(123);
rand_num = rand(1, 2) # generate a random number matrix
srand(345); 
rand_num_new = rand(1, 2)

printf( "\n");

# Case 2: use the same random number seed
# The matrix rand_num will be same as matrix rand_num_new.
srand(123);
rand_num = rand(1, 2)
srand(123);
rand_num_new = rand(1, 2)

Result:

rand_num =
 0.00227290671   0.935245633
rand_num_new =
 0.00640942669     0.4539437

rand_num =
 0.00227290671   0.935245633
rand_num_new =
 0.00227290671   0.935245633

See also
rand

meshgrid

Description
Generates rectangular grid in 2-D or 3-D space.
Used in FDTD and FDE.

Syntax

Code	Function
`[X1,X2] = meshgrid(x1,x2)`	Generates 2D rectangular grid using vectors x1, x2.
`[X1,X2,X3] = meshgrid(x1,x2,x3)`	Generates 3D rectangular grid using vectors x1, x2, x3.

See also
ndgrid

ndgrid

Description
Generates rectangular grid in N-D space.
Used in FDTD and FDE.

Syntax

Code	Function
`[X1,X2,...,Xn]=ndgrid(x1,x2,...,xn)`	Generates N-D rectangular grid using vectors x1, x2, ..., xn.
`[X1,X2,...,Xn] = ndgrid(xg)`	Specifies a single grid vector xg to use for all dimensions. The number of output arguments you specify determines the dimensionality n of the output.

Example
Example 1: Create 2-D Grid
code:

[X, Y] = ndgrid(1:2:19,2:2:12);

Result:

>X
X =
             1             1             1             1             1             1
             3             3             3             3             3             3
             5             5             5             5             5             5
             7             7             7             7             7             7
             9             9             9             9             9             9
            11            11            11            11            11            11
            13            13            13            13            13            13
            15            15            15            15            15            15
            17            17            17            17            17            17
            19            19            19            19            19            19
>Y
Y =
             2             4             6             8            10            12
             2             4             6             8            10            12
             2             4             6             8            10            12
             2             4             6             8            10            12
             2             4             6             8            10            12
             2             4             6             8            10            12
             2             4             6             8            10            12
             2             4             6             8            10            12
             2             4             6             8            10            12
             2             4             6             8            10            12

Example 2: xg — Grid vector for all dimensions
code:

[a, b] = ndgrid([1,2,3]);  # same as [a, b] = ndgrid([1,2,3],[1,2,3]);

Result :

>a
a =
             1             1             1
             2             2             2
             3             3             3
>b
b =
             1             2             3
             1             2             3
             1             2             3

See also
meshgrid

size

Description
The size function returns the size of the input argument.
Used in FDTD and FDE.

Syntax

Code	Function
`size( A )`	Returns the size of the object A.

For different object, size function returns different result:

numeric
size returns a matrix whose 1st element is the number of rows, and whose 2nd element is the number of columns.
struct
For struct input, size returns number of elements of struct.
cell
For cell input, size returns a matrix whose 1st element is the number of rows, and whose 2nd element is the number of columns.

See also
length, show

length

Description
Returns the length of an object.
Used in FDTD and FDE.

Syntax

Code	Function
`out = length ( A );`	Returns the length of an object A. The parameter A can be vector, matrix(returns `max (size ( A ))`), struct(returns number of elements) or cell.

For different object, length function returns different result:

numeric
For numeric input like matrix, length returns max( size(A) ).
struct
For struct input, length returns number of elements of struct.
cell
For cell input, length returns max( size(A) ).

Example

b = rand(2,3);
out = length(b) # return max( size(b) )

Result:

out = 
        3

See also
size

sizeof

Description
The sizeof function returns the number of bytes of data in the argument A.
Used in FDTD and FDE.

Syntax

Code	Function
`out = sizeof ( A )`	Returns the size of an object in bytes.

See also
size, who, whos

squeeze

Description
Removes singleton dimensions.
Used in FDTD and FDE.

Syntax

Code	Function
`squeeze(A)`	Returns an array with the same elements as A, but with all singleton dimensions removed.

Example

code:

a=[1,2,3]
a(:,:,2) = [4,5,6]  # matrix size is 1-3-2 
b=squeeze(a)        # matrix size is 3-2

Result:

a =
             1             2             3
a(:,:,1) =
             1             2             3

a(:,:,2) =
             4             5             6
b =
             1             4
             2             5
             3             6

reshape

Description
reshape does what its name implies, it reshapes the input matrix so that the return value has the number of rows and columns specified by the last two arguments. reshape will not reshape the matrix if the product of the new row and column dimensions does not equal the product of the existing row and column dimensions.

Used in FDTD and FDE.

Syntax

Code	Function
`B = reshape ( A, sz )`	Returns a new matrix B from A reshaped by a vector sz.
`out = reshape ( A, sz1, ... szN )`	Returns a new matrix B from A reshaped by sz1, ... szN.

Examples

m = [7,8,9;1,2,3;4,5,6;7,8,9];

n1 = reshape(m,2,6);
n2 = reshape(m,[6,1,2]);

szn1 = size(n1)
szn2 = size(n2)

Result:

szn1 =
             2             6
szn2 =
             6             1             2

rot90

Description
B = rot90(A) is the 90 degrees counterclockwise rotation of matrix A.
Used in FDTD and FDE.

If A is an N-D array, rot90(A) rotates in the plane formed by the first and second dimensions, rot90(A,K) is the K * 90 degrees rotation of A, K = +-1,+-2,...

Syntax

Code	Function
`B = rot90(A)`	Rotates array A 90 degrees.
`B = rot90(A, K)`	Returns B which is the K * 90 degrees rotation of A.

See also
flip

indexbyxy

Description
Returns designated elements according to input vectors x, y.
Used in FDTD and FDE.

The indexbyxy function will call the sort function to sort x, y and get the index
information ( y.ind, x.ind ) returned by sort function. Then returns the elements indexed by y.ind, x.ind, namely fyx(y.ind, x.ind).

Syntax

Code	Function
`out = indexbyxy(y, x, fyx);`	Returns designated elements according to input vectors y, x.

Example

fyx = rand(3,3)
y = [1, 3, 2];
x = [1, 2];

out = indexbyxy(y, x, fyx)

Result:

fyx =
   0.225171864   0.400170177   0.252445549
   0.861157596   0.995036304   0.926949918
    0.63800782   0.225752905     0.1726145
out =
   0.225171864   0.252445549   0.400170177
   0.861157596   0.926949918   0.995036304

基础数学

abs #

angle #

real #

imag #

conj #

pow #

dot #

cross #

cumprod #

cumsum #

all #

any #

iscolumn #

isrow #

ceil #

fix #

floor #

round #

int #

max #

maxi #

min #

mini #

findpeaks #

sort #

sort2 #

flip #

inf #

nan #

mod #

prod #

rem #

sign #

acos #

asin #

atan #

atan2 #

cos #

sin #

tan #

acosd #

asind #

atand #

atan2d #

cosd #

sind #

tand #

log #

log10 #

exp #

frexp #

ldexp #

sqrt #

sum #

union #

complement #

intersection #

compan #

cart2cyl #

cart2sph #

sph2cart #

cyl2sph #

linspace #

logspace #

eye #

ones #

zeros #

rand #

srand #

meshgrid #

ndgrid #

size #

length #

sizeof #

squeeze #

reshape #

rot90 #

indexbyxy #

本页目录

abs

angle

real

imag

conj

pow

dot

cross

cumprod

cumsum

all

any

iscolumn

isrow

ceil

fix

floor

round

int

max

maxi

min

mini

findpeaks

sort

sort2

flip

inf

nan

mod

prod

rem

sign

acos

asin

atan

atan2

cos

sin

tan

acosd

asind

atand

atan2d

cosd

sind

tand

log

log10

exp

frexp

ldexp

sqrt

sum

union

complement

intersection

compan

cart2cyl

cart2sph

sph2cart

cyl2sph

linspace

logspace

eye

ones

zeros

rand

srand

meshgrid

ndgrid

size

length

sizeof

squeeze

reshape

rot90

indexbyxy