Preface

The Wilkinson power divider is a three-port device used for power distribution. Compared to a conventional T-junction power divider, it can match the impedance of all ports and distribute power in any ratio. Unlike resistive power dividers, the Wilkinson power divider not only can isolate the output ports but also indicate no loss when the ports are matched, only dissipating reflections from the output ports. This case models and simulates an equal-split (3 dB) Wilkinson power divider designed in Example 7.2 from Pozar ^[1].

Simulation settings

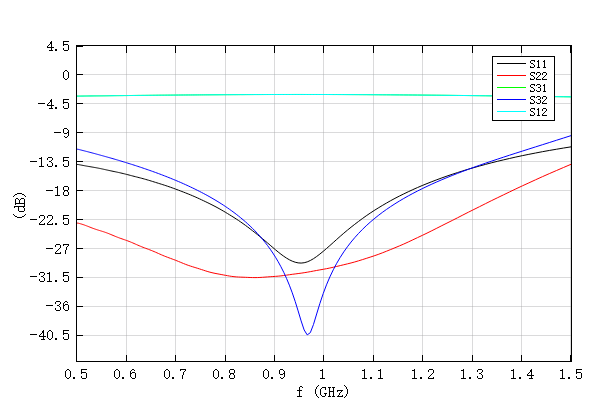
Device construction

The structure of the Wilkinson power divider used in this case is shown in the figure above, where $Port 1$ is the input port and $Port 2$ and $Port 3$ are the output ports. The entire structure consists of metal transmission lines(TLs) and the resistor placed on a substrate, with a substrate thickness of $d=1.59mm$ and a relative permittivity of $\epsilon_r=2.2$. Formula 3.196 in Pozar ^[1:1] describes the dimensions and characteristic impedance of the microstrip TL as follows:

$Z_0=\begin{cases} \frac{60}{\sqrt{\epsilon_e}}In(\frac{8d}{w}+\frac{w}{4d}) &w/d \leq 1 \\ \frac{120 \pi}{\sqrt{\epsilon_e}[w/d+1.393+0.667In(w/d+1.444)]} &w/d \geq 1\end{cases}$

Where $w$ is the width of the TL, $d$ is the substrate thickness, and $\epsilon_e$ is the effective permittivity of the microstrip TL. The effective permittivity of the microstrip TL is approximately:

$\epsilon_e=\frac{\epsilon_r +1}{2}+\frac{\epsilon_r -1}{2}\frac{1}{\sqrt{1+12d/W}}$

Where $\epsilon_r$ is the relative permittivity of the substrate. Based on the above formulas and the characteristic impedance values of each TL, the width $w$ of each TL can be calculated, which are $4.9mm (Z_0=50\Omega)$ and $2.804mm (\sqrt{2}Z_0=70.7\Omega)$, respectively.

The thickness of the TLs and the resistor is much smaller than the operating wavelength, so 2D structure can be used for modeling. The ring TL with an impedance of $\sqrt{2}Z_0$ can be formed from 2D polygon, with a circumference of $55.5mm$. The resistor is modeled using a 2D rectangle with lumped $<RLC>$ material, with the current direction along the $X$ axis and a resistance value of $R=100\Omega$.

Source

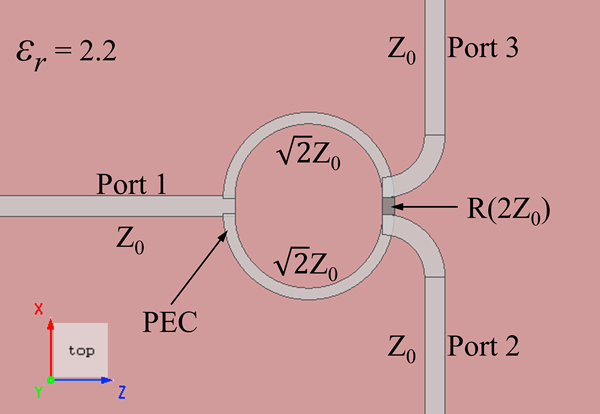
In this case, the Port group is used as the input source, with three ports added at the positions of $Port 1$, $Port 2$, and $Port 3$ in the figure above. The design frequency of this device is $f=1GHz$, so we set the frequency range of the light source to $0.5-1.5GHz$.

The S-parameters of a three-port device consist of nine elements, as follows:

$S=\begin{bmatrix} S_{11} & S_{12} & S_{13} \\ S_{21} & S_{22} & S_{23} \\ S_{31} & S_{32} & S_{33} \end{bmatrix}$

To obtain all the S-parameter components of the device, multiple simulations are required. Due to the reciprocity ($S_{ij}=S_{ji}$) and symmetry of the device, only two simulations are needed to determine all the S-parameters. The two simulations are carried out with $Port 1$ and $Port 2$ as the source ports.

Solver settings

The $Y_{min}$ boundary of the solver uses the PEC boundary condition to simulate the ground plane of the device, while the remaining boundary conditions are all PML. When $Port 1$ is used as the input source, due to the symmetry of the source and the structure, we can use the Symmetric boundary condition at $X_{min}$ to reduce the simulation region to half, thereby reducing the simulation time, as shown in the figure below.

Simulation results

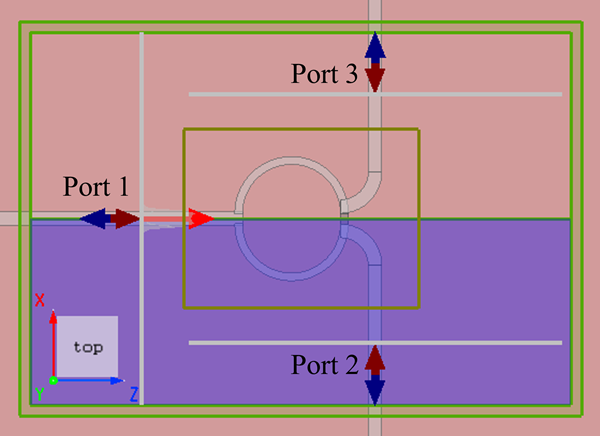
Electric field distribution

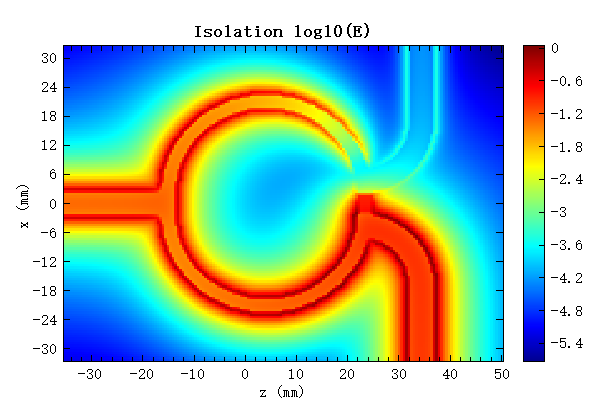
The figure below shows the electric field distribution of the device at a frequency of $1GHz$ during transmission and isolation simulations. When $Port 1$ is used as the source port, due to symmetry, the electric field intensities at $Port 2$ and $Port 3$ are identical. When $Port 2$ is used as the source port, the electric field intensity at $Port 3$ is low, demonstrating significant isolation between $Port 2$ and $Port 3$.

S parameter

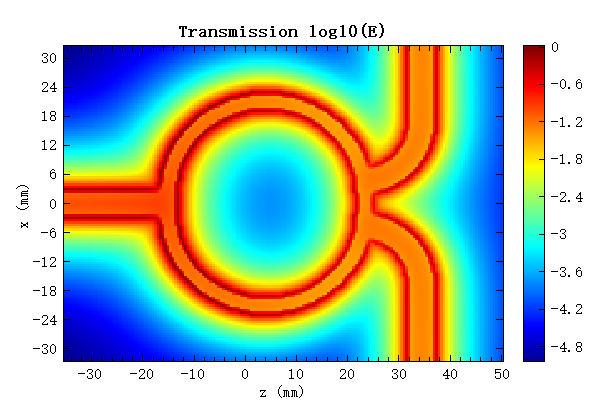
The S-parameters of the Wilkinson power divider are shown in the figure below. Its center frequency is $0.966GHz$, which is less than 4% different from the design frequency of $1GHz$. At a frequency of $1GHz$, $S_{11}=-27dB$ and $S_{22}=-30dB$, indicating that the reflections from any input port are very small at the design frequency, which means good impedance matching between the ports. $S_{32}=-33dB$ shows that the power transmitted from $Port 2$ to $Port 3$ is very small, indicating good isolation between the output ports; $S_{31}=-3.05dB$, with less than 10% variation across the entire simulation frequency band, indicates that the power transmitted from the input port ($Port 1$) to $Port 3$ is approximately 50% across the entire band. Due to the symmetry of the device, the power transmitted from the input port to $Port 2$ is also 50%, demonstrating the equal power distribution and good bandwidth of the device.

References

---

1. D. M. Pozar, Microwave Engineering, Fourth Edition. John Wiley & Sons (2012). ↩︎ ↩︎