基于石墨烯的可调谐太赫兹超材料
前言
石墨烯是厚度为一个原子的单层碳材料,由于其独特的物理特性,可以被应用于纳米级等离激元系统。通过调整静电掺杂或费米能级来激发单层石墨烯的表面等离激元波,从而实现对光的操纵和控制。
Chu[1]等人研究了一种基于单层和多层掺杂的石墨烯可调谐的太赫兹超材料。他们发现石墨烯层数和费米能级的轻微变化,可以使共振波长和调制强度发生显著改变。本案例将仿真该调谐过程。
仿真设置
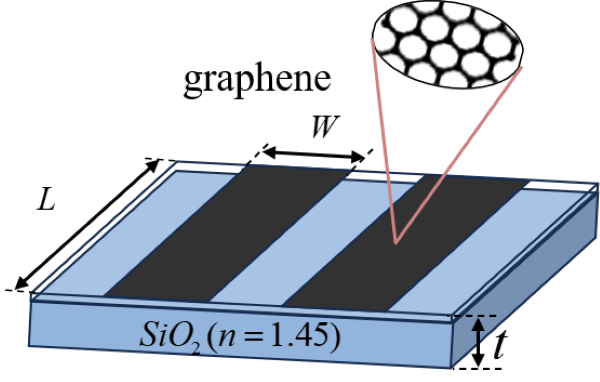
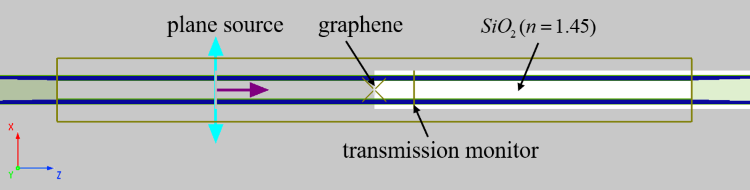
本案例使用 3D FDTD 进行仿真。石墨烯沉积在硅衬底上,沿 x 轴边长 , 沿 y 轴的边长为 , 二氧化硅衬底的厚度为 。结构在 X 和 Y 方向上均匀无限延伸,故使用周期性边界条件来节约仿真时间。在 z 方向上使用 PML 边界条件,将 PML 层数设置为 12 来提高对光的吸收效果。其仿真示意图如下所示。同时,由于石墨烯结构非常微小,因此对石墨烯层使用自定义网格以提高仿真精确度。
材料
- Graphene
关于石墨烯材料参数的具体细节详见Graphene。
石墨烯超材料工程仿真时,使用下表中的四组参数来探究石墨烯层数和费米能级改变时共振波长和调制深度的变化。
| Number | Scattering Rate() | Chemical Potential(/eV) | Temperature(T/K) | Conductivity Scaling(c) |
|---|---|---|---|---|
| 1 | 0.00102 | 0.265 | 300 | 1 |
| 2 | 0.00102 | 0.265 | 300 | 4 |
| 3 | 0.00099 | 0.217 | 300 | 1 |
| 4 | 0.00099 | 0.217 | 300 | 4 |
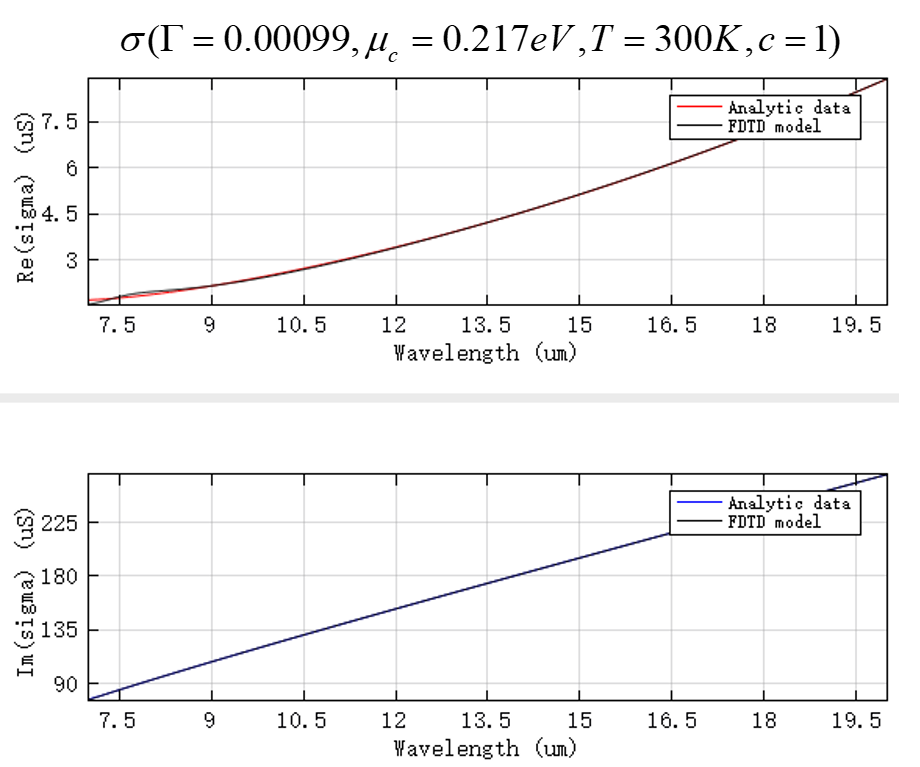
当以上参数取 ; ; ; ,可以得到石墨烯表面电导率的拟合结果,其实部和虚部如下图:
仿真结果
本案例中,石墨烯使用了 0.265eV 和 0.217eV 两个化学势(即费米能级),石墨烯层数使用了 1 和 4。材料参数参考[1:1]中的设置,该文章当中石墨烯为近似 Drude 的模型,本案例中石墨烯材料由包含带内电导和带间电导的全表面电导模型进行拟合。
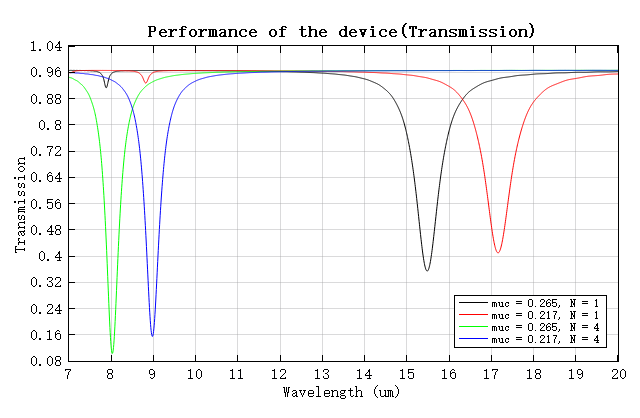
打开附件工程,并运行Graphene_metamaterial.msf脚本,即可获得对应不同石墨烯费米能级和层数的透射率(见下图),该结果与参考文献[1:2]图 3(a)所示的结果非常匹配。仿真结果显示石墨烯费米能级的增加会使共振波长蓝移,调制强度也会随着石墨烯层数的增加而增加。
附录
近似 Drude 模型石墨烯电导率[1:3]:
为角频率, 为电子弛豫时间, 为费米能级。
该模型材料省略了带间电子跃迁对电导率的贡献。在上述嵌套扫描结束后,运行脚本Graphene_conductive.msf可以获得 Drude 模型石墨烯和全表面电导模型石墨烯表面电导率的实部和虚部,两者的表面电导率有一定的差别。



