前言 #

单模光纤相对于多模光纤纤芯更细，在工作波长范围内仅允许单个模式传输，这种设计为其提供了优异的传输性能和可靠性。单模光纤广泛应用于通信领域，包括长距离光纤通信、数据中心互连、无线基站回传、CATV、光纤传感等。本案例将以康宁SMF-28 单模光纤为例展示简单的模式计算。

仿真设置 #

本案例将使用 FDE 2D 仿真进行解模，其仿真结构如下图，相关参数见下表。在 FDE 的最小 x、z 方向上使用对称/反对称边界条件，它可以在求解过程忽略不满足对称性要求的模式，便于快速求解具有特定对称性的模式。具体细节请参考boundary conditions。

符号	尺寸	折射率
$r_{core}$	$4.1\mu m$	1.44
$R_{cladding}$	$50 \mu m$	1.434816

仿真结果 #

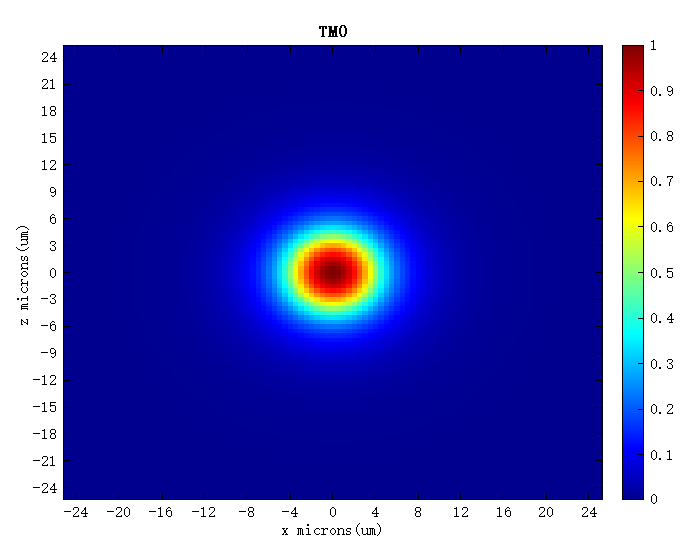
打开附件工程，在 FDE 当中，设置 $1.55\mu m$ 的中心波长，运行Model analysis，解模结果中的第一个模式即为基模，其模式轮廓图如下图所示

下面研究 SMF-28 光纤的传输特性。此时禁用对称/反对称边界条件，将边界都设置为 PEC，切换到Frequency sweep analysis，波长范围设置为光通信波段 $1.26\mu m - 1.66\mu m$。运行结束后，得到基模等效折射率随波长变化的趋势，如下图所示。对于基模来说，其等效折射率在整个波长范围内都大于包层折射率，因此基模被很好地限制在纤芯中。

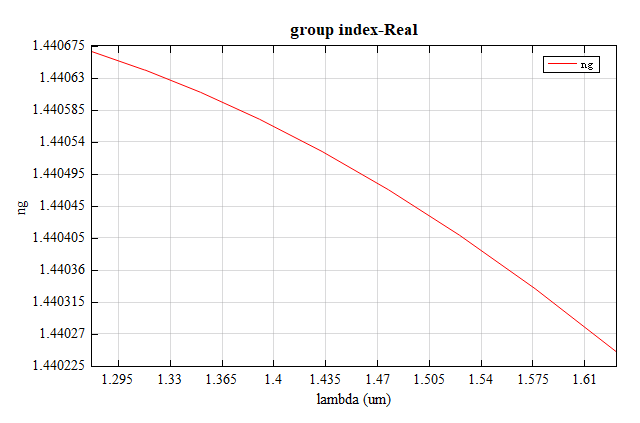
除此之外，光脉冲在光纤中传输的群速度对于信号延时/信号保真度也是极其重要的参数，根据折射率定义可以计算其群折射率为 $n_g=c/v_g$，在结果当中可以绘出基模的群折射率随波长变化的曲线，如下图所示。

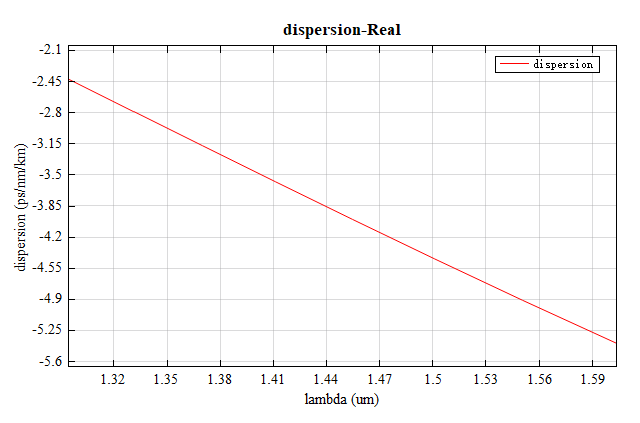
由上述结果可以观察到，模式光源在不同频率下其群速度并不相同，这将带来模式色散，在结果当中绘制模式色散图如下图所示。可以看到 SMF28 光纤的基模在整个频率范围内拥有较低的色散系数，这使其拥有了长距离传输信号的能力，能有效避免信号失真。