Preface
Arrayed waveguide gratings (AWGs) are essential components in dense wavelength division multiplexed (DWDM) systems. As large-scale photonic integrated devices continue to evolve, the miniaturization design of AWGs has become an important topic. Silicon nanowires, with their high contrast of refractive index between the core and cladding, allow light to be confined within smaller waveguides, which enables the smaller curvature radius with same bending loss and decreased spacing between arrayed waveguides under the same crosstalk. As a result, silicon-based AWGs become a good candidate technology to facilitate the (de)multiplexer integration.
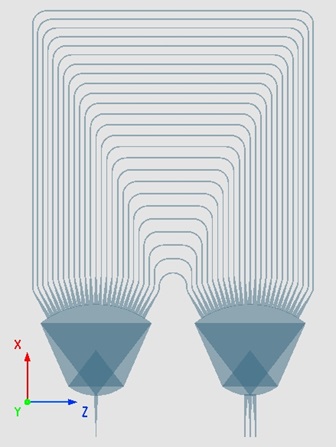
In this example, a 2.5D-FDTD solver was employed to simulate a saddle-shaped silicon nanowire AWG to investigate its output spectral response and loss, as depicted in the figure. Due to the large structural dimensions of AWGs, 3D-FDTD simulations consume significant computational resources and cost long simulation time. In contrast, 2.5D-FDTD employs the equivalent materials since the structure remains same in the vertical direction, transforming the 3D problem into a 2D problem. Thus, the simulation can be greatly simplified while keeping similar simulation accuracy.
Simulation settings
Structure
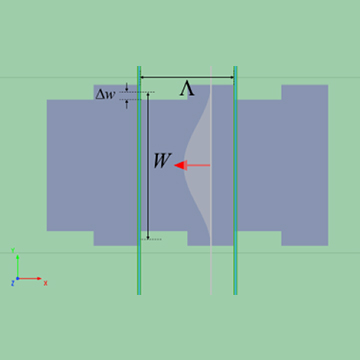
In this example, the design of the Si-AWG is referenced from the publication[1] and employs one input waveguide and three output waveguides. The design assumes three conditions: (1)Material parameters are taken from the TE fundamental mode at central wavelength at room temperature; (2)The diameter of the Roland circle is significantly larger than the core-to-core distance at the input/output couplers of AWGs; (3)The difference in effective refractive index and group refractive index between the curved waveguide and the straight waveguide can be neglected. The structure used in this example is illustrated in the figure below, with a working central wavelength of and a channel spacing of .
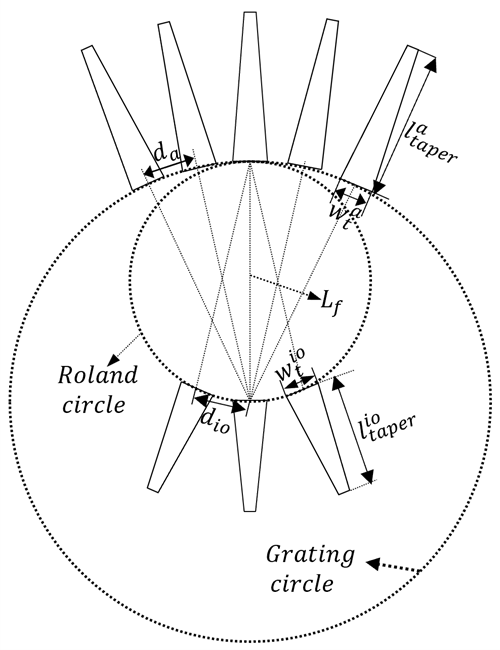
| variables | symbol | value |
|---|---|---|
| Free spectral width | ||
| Straight waveguide width | ||
| Number of arrayed waveguide | ||
| Core-core distance of each input/output/array waveguide | , | |
| Width of the taper connecting the arrayed waveguide and planar waveguide at the grating circle | ||
| Width of the taper connecting the input/output waveguides and the planar waveguide at the Roland circle | ||
| Length of taper | ||
| Length of input/output waveguide | ||
| Radius of bending waveguide | ||
| Length of the straight waveguide in the shortest array waveguide | ||
| Diameter of Roland circle | ||
| Adjacent array waveguide length difference |
Solver settings
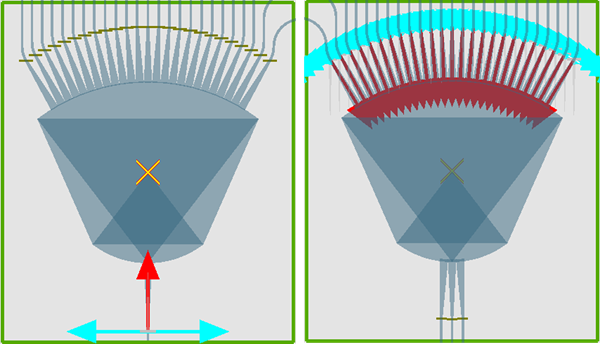
For Si_AWG, the part of arrayed waveguide contains only waveguide structures that support stable transmission and generate phase delays in each channel. Consequently, the each part of arrayed waveguide grating can be simulated separately: the input planar waveguide and the output planar waveguide, as shown below. So the simulation region can be greatly reduced, leading to much shorter simulation time.
Source
Since we separate the AWG simulation into two parts, the light source for each arrayed waveguide in the output region must be guaranteed to be the same as the mode of each arrayed waveguide coupled by the light source through the input planar waveguide. From the above figure, we observe that the light is injected to the output tapered waveguide with a certain angle after passing through the arrayed waveguide. Therefore, we should align the injection direction of the mode sources with the middle axis angle of the tapered waveguides. Our mode solver will automatically calculate the propagation mode in the current direction.
We also need to set the amplitude of each mode source to match the transmittance of light coupled from the input waveguide into each individual waveguide in the array. And the pulse delays of each mode source should be computed based on the phase delays from length differences in arrayed waveguide. Thus, the pulse delay of the mode source can be calculated as follows:
where is the length difference between neighboring array waveguides, is the group refractive index of the array waveguide, and is the speed of light in vacuum.
Simulation results
Input planar waveguide region
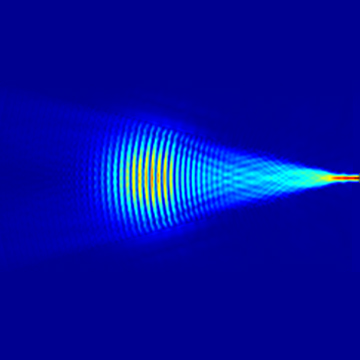
The FDFP monitor placed within the silicon substrate records the electric field distribution at a wavelength of as light propagates from the input waveguide into the arrayed waveguide. From the diagram below, we observe that light couples from the input waveguide to the input planar waveguide region, undergoes beam expansion, freely propagates to the edge of the Roland circle, and subsequently couples into the arrayed waveguide.
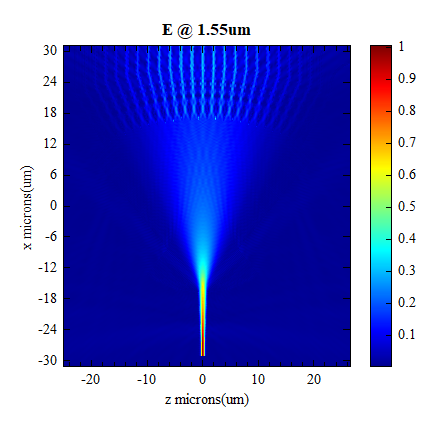
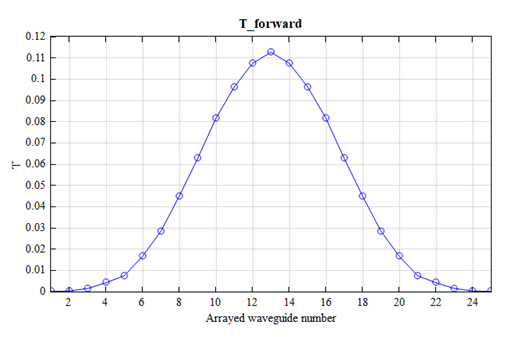
The figure below shows the transmission rates within each of the 25 tapers placed at the top of the arrayed waveguide and oriented perpendicular to the waveguide, which indicates that most of the injected energy is effectively coupled into the arrayed waveguide.
Output planar waveguide region
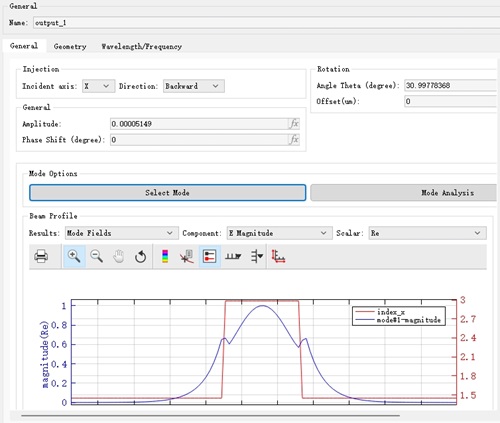
The mode injected by the leftmost mode source as shown below. You can see that the mode source is still correct when it is angled.
The electric field distribution of light with a wavelength of , obtained from the FDFP monitor placed inside the silicon substrate, is depicted in the figure below. Multiple channels of light enter the arrayed waveguide, couple into the Roland circle, and undergo diffraction. Eventually, at the edge of the output waveguide, they converge into a strong beam, which couples into the output waveguide. Adjacent to the strongest diffracted light, there are two weaker diffraction beams corresponding to diffraction orders .

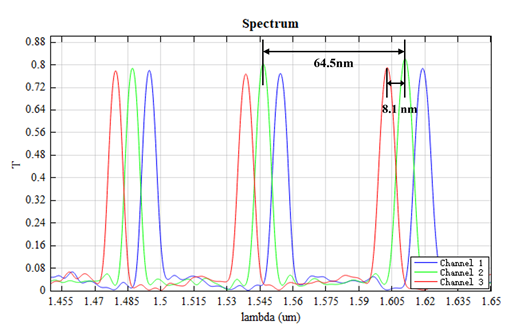
The transmission rate of three output waveguides as a function of wavelength is shown in the figure below. This AWG exhibits a channel spacing of and a free spectral width of , which aligns with the design specifications.
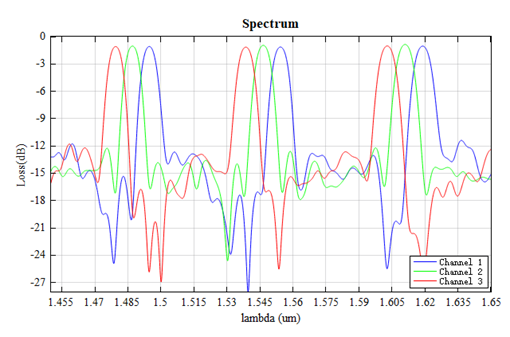
The figure below illustrates the loss of the three output waveguides as a function of wavelength obtained from the FDFP monitors. Notably, the device exhibits an insertion loss of and crosstalk levels below .
References
Huamao H. Research on arrayed waveguide gratings based on silicon nanowires[D]. Huazhong University of Science and Technology, 2010. ↩︎