Preface

The human eye perceives specific colors in response to specific light spectra. Reflective color filters are used to selectively modulate reflection spectra to provide different color perceptions to the human eye. According to the study conducted by Yang ^[1] et al., a reflective color filter base on a $Ni/SiO_2/Al$ asymmetric Fabry-Perot (FP) cavity was modeled and simulated. The $Ni$ layer exhibits a near-perfect absorption effect across the solar spectrum. If the appropriate thickness is selected, the $Al$ layer blocks light transmission. By adjusting the thickness of the $SiO_2$ intermediate layer, a reflection spectrum is achieved that allows the human eye to perceive vibrant colors with high saturation and brightness. This case demonstrates how to calculate the chromaticity coordinates related to the reflection spectrum, and further analyzes the color adjustment patterns of the color filter.

Simulation Settings

In 2D FDTD simulation, the color filter has a simple three-layer film structure, with the top layer made of $Ni$ , the intermediate layer made of $SiO_2$ , and the bottom layer made of $Al$ . The simulation of natural lighting conditions involves using a planar source in the wavelength range of $0.38\mu m$ ~ $0.78\mu m$ , with incident rays perpendicular to the negative z-axis, as shown in the figure below. As the structure expands periodically along the x-axis and the polarization of the source is parallel to the x-axis, X axis min and X axis max are set to Anti-Symmetric boundaries to speed up simulation calculations. It is important to note that due to the small thickness of the $Ni$ top layer, a custom refined mesh is used for this layer to improve the accuracy of simulation results.

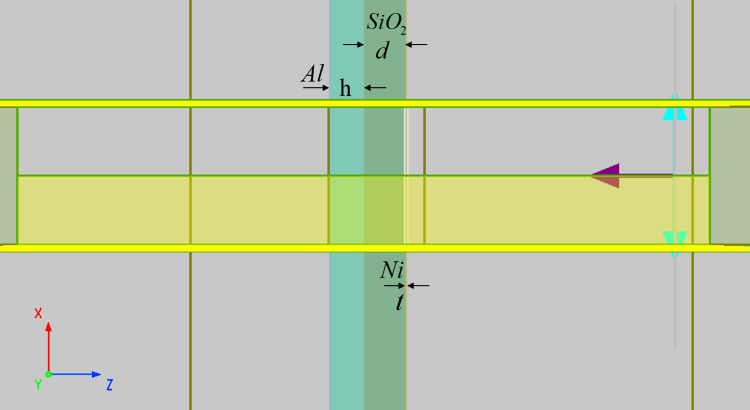
structure

Parameter	Dimension
$t$	$6 nm$
$d$	$120 nm$
$h$	$100 nm$

Material

$Ni$

The material of the top layer is taken from the built-in material library and is therefore subject to fitting within the visible light wavelength range ( $0.38\mu m$ ~ $0.78\mu m$ ). The fitting results are shown in the figure below.

$SiO_2$

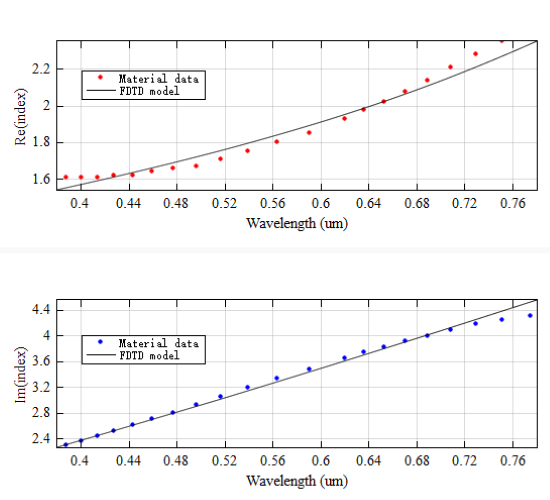
The intermediate layer is made of $SiO_2$ and can be approximated as a dielectric material with a refractive index of $1.46$ within the wavelength range of $0.38um$ ~ $0.78um$ .
$Al$

The material of the bottom layer is taken from the built-in material library and is therefore subject to fitting within the visible light wavelength range ( $0.38\mu m$ ~ $0.78\mu m$ ). The fitting results are shown in the figure below.

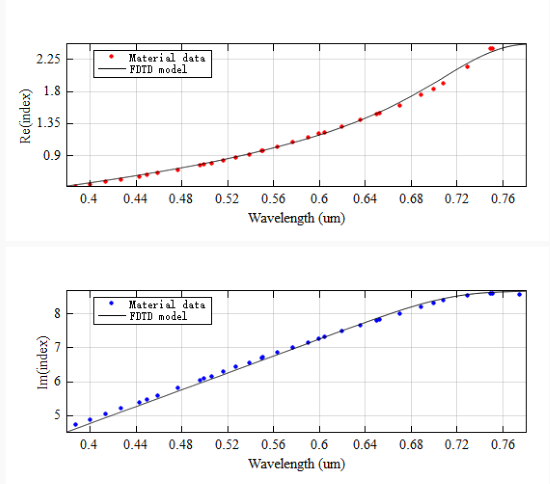
Simulation Results

After opening and running the attached project, the FDFP Monitor displays the electromagnetic field, power, and other physical quantities within the full range of $0.38\mu m$ ~ $0.78\mu m$ . The electric field distribution at the wavelength $0.38\mu m$ , as shown below, reveals a distinct local enhancement of the electric field caused by the FP cavity effect. This enhancement leads to almost all the energy being absorbed by the top $Ni$ layer, which exhibits a near-perfect absorption effect. Due to the transmission blocking of the $Al$ layer, the electromagnetic waves are confined in the asymmetric Fabry-Perot cavity.

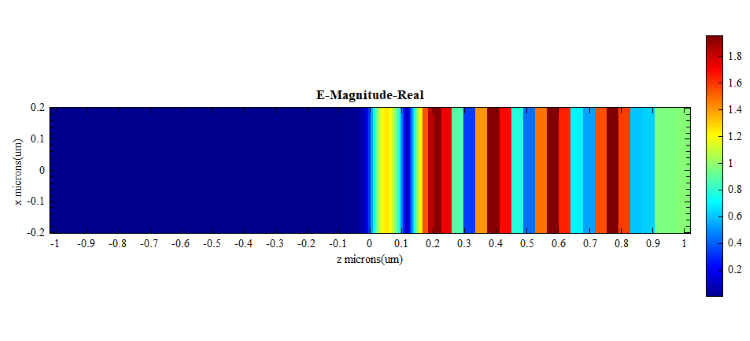
FDFP_monitor

Parameter analyses

Reflection Spectrum and Chromaticity Coordinates

After opening the attached project, executing the parameter sweep d_120_270_50nm, and setting the thickness $d$ of the $SiO_2$ middle layer to $120nm$ , $170nm$ , $220nm$ , and $270nm$ respectively, the swept reflectivity results are obtained, as shown in the figure below. By running the script Reflective_Color_Filters.msf, the CIE chromaticity coordinates are calculated according to the reflection spectrum, and the colors associated with these chromaticity coordinates are determined as shown in the figure. Furthermore, the reflection spectrum is analyzed to identify the peaks at wavelengths of $0.395\mu m$ , $0.535\mu m$ , $0.676\mu m$ , and $0.417\mu m$ . The above results are consistent with Figure 1 given in the reference.

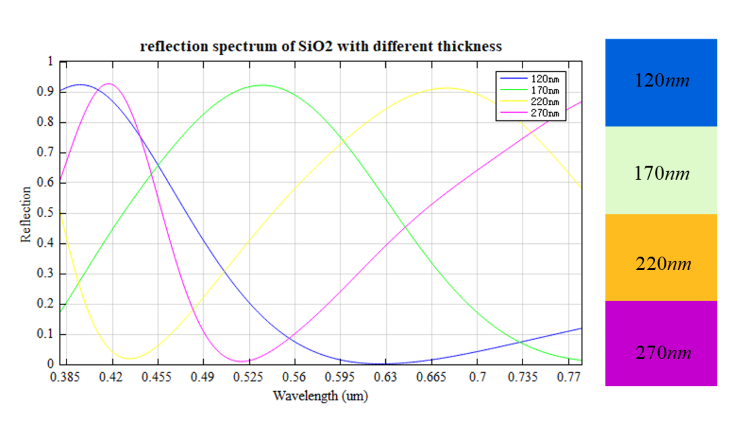
ref_sepectrum

Reflection Spectrum with middle Layer Thickness Sweep

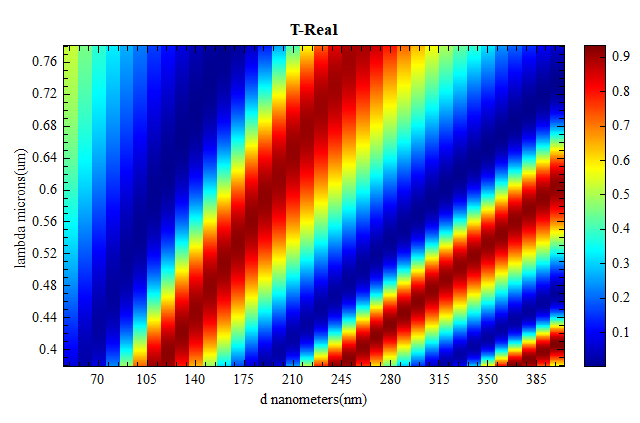
After opening the attached project and executing the parameter sweep d_50_400_10nm, the continuous correlation between the reflection spectrum $R$ and the thickness $d$ of $SiO_2$ layer is obtained, as shown in the figure below. The $SiO_2$ layer with a thickness $d$ of $50nm$ ~ $80nm$ exhibits lower reflectivity within the visible light wavelength rang. As the thickness $d$ increases continuously from $80nm$ to $240nm$ , the position of the reflection peak experiences a red shift, moving from $0.38\mu m$ to $0.78\mu m$ . In addition, when the thickness $d$ exceeds $250nm$ and $360nm$ , two high-order modes become noticeable at a wavelength of $0.38\mu m$ . These results are consistent with Figure 2 given in the reference.
Therefore, the position of the reflection peak can be continuously fine-tuned by varying the thickness $d$ of the $SiO_2$ intermediate layer. This means that the color filter can produce colors with high saturation and brightness across the entire visible light range.

ref_sepectrum_sweep

Appendixes

The contour coverage of the chromaticity diagram represents the gamut range of all physically possible colors in nature. According to the CIE standard colorimetric system established by the International Commission on Illumination (CIE), the chromaticity coordinates of the reflection spectrum are calculated as follows:

The spectral power distribution is expressed as:

$P(\lambda)=I(\lambda)R(\lambda)$

Wherein, $I$ ( $\lambda$ ) represents the relative radiation spectrum of the white light source, and $R$ ( $\lambda$ ) represents the reflection spectrum. The tristimulus values $X$ , $Y$ , and $Z$ are calculated using the following equations:

$X=\frac{1}{K}\int_\lambda \bar{x}(\lambda)P(\lambda)d\lambda$

$Y=\frac{1}{K}\int_\lambda \bar{y}(\lambda)P(\lambda)d\lambda$

$Z=\frac{1}{K}\int_\lambda \bar{z}(\lambda)P(\lambda)d\lambda$

Wherein, $\bar{x}$ , $\bar{y}$ , $\bar{z}$ are standard observer functions. The integral is taken over the visible light range of $0.38um$ ~ $0.78um$ , and $K$ is the normalization constant:

$K=\int_\lambda \bar{y}(\lambda)I(\lambda)d\lambda$

The CIE chromaticity coordinates ( $x$ , $y$ , $z$ ) can be obtained through normalization as follows:

$x=\frac{X}{X+Y+Z}$

$y=\frac{Y}{X+Y+Z}$

$z=\frac{Z}{X+Y+Z}=1-x-y$

Due to the normalization of the incident source intensity, the coordinates ( $x$ , $y$ , $z$ ) are represented by only two independent values.

References

Yang Z , Zhou Y , Chen Y , et al. "Reflective Color Filters and Monolithic Color Printing Based on Asymmetric Fabry–Perot Cavities Using Nickel as a Broadband Absorber".Advanced Optical Materials,(2016) ↩︎