Preface

In recent years, the unusual dispersion properties of photonic crystals (PCs), including the superlens, self-collimation (SC), and negative refraction, have attracted more and more interest and become an active research area. The SC achieves collimated radiation with almost no diffraction effect when the incident light propagates along a particular direction of the crystal. Line defects in 2D PCs cause bending and splitting of the SC beam. In this example, the effect of "optical switching" can be achieved by altering the line defects (radius of the dielectric rod) in the photonic crystal.

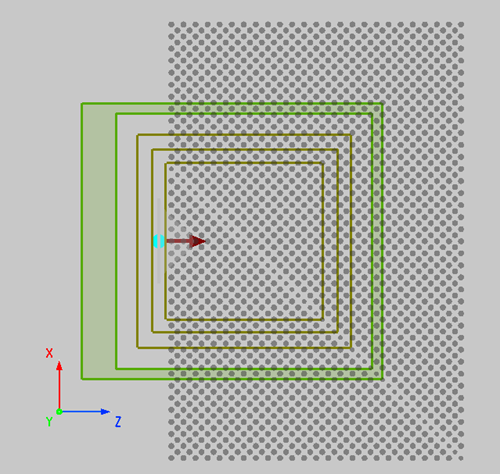
Simulation settings

The 2D PC used in this example is composed of dielectric rods of radius $0.35\mu m$ and a dielectric constant of 12. The lattice constant is $a = 1 \mu m$ and Perfectly Matched Layers (PML) are used on all boundaries. By controlling the radius of the dielectric rods on the diagonal of the simulation region, we can create a linear defect in this crystal. From Ref^[1], we know that the SC phenomenon occurs at the wavelength around $\lambda=a/0.194$ and propagates along the lattice direction of this crystal. So we use a Gaussian beam with wavelength $5.15464\mu m$ incident from the left side of the crystal.

Simulation results

As shown in the figure below, when the radius of the dielectric rods on the diagonal is $0.35\mu m$, the PC is perfect periodic, and there is almost no diffraction phenomenon when the beam propagates along it; when the radius of the dielectric rods on the diagonal is 0, the beam is completely reflected at the diagonal (the line defect). The result reproduces figure 2 of the Ref, demonstrating that the power ratio between the two splitted beams can be very well controlled by varying the radius of the defect rods.

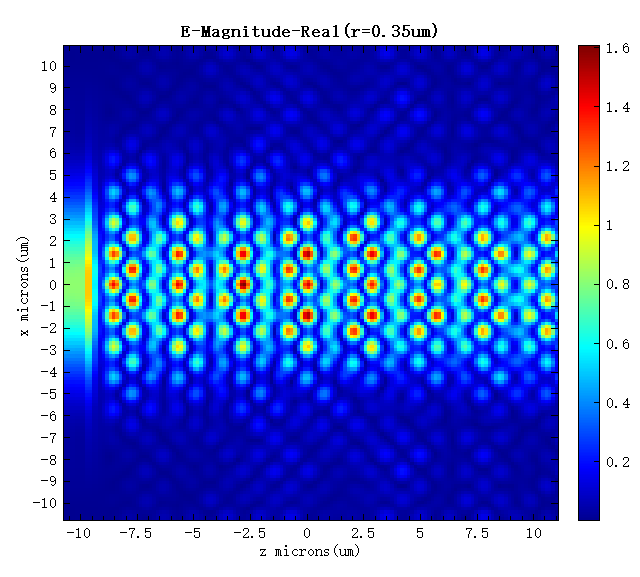
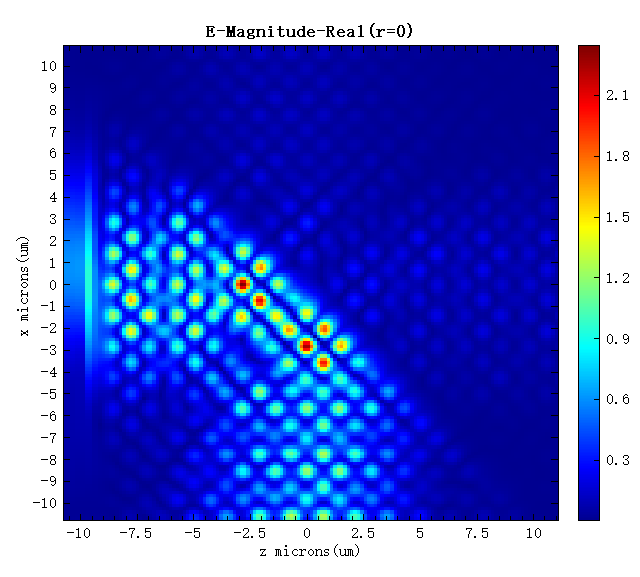
Parameter analyses

Run the parametric sweep of dielectric rods radius to study the effect of line defects of the PC. We can plot the normalized reflected/transmitted power as a function of the defect radius.

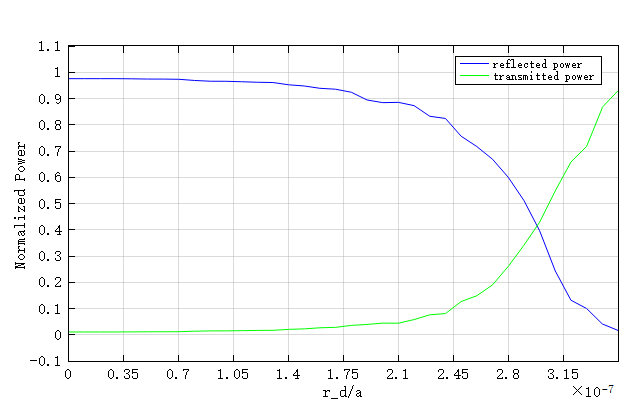
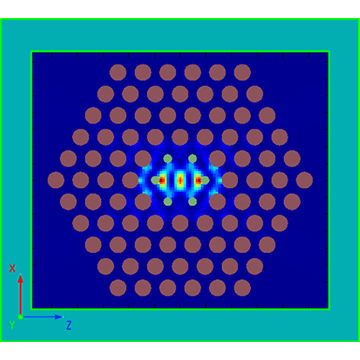
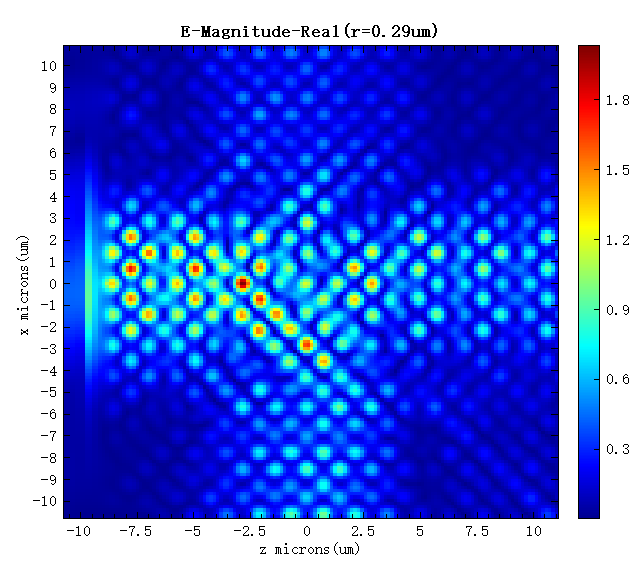
As shown in the above figure, when the defect radius $r=0\mu m$, the beam passing through the structure is almost completely reflected at the line defect; when the defect radius $r=0.29\mu m$, the beam passing through the structure is half-reflected and half-transmitted; with the gradual increase of the defect radius to $r=0.35\mu m$, the PC is changed into a perfect periodic PC, and the beam passing through the structure can be completely transmitted. Therefore, by adjusting the defect radius, we can manipulate the propagation direction of the light beam to achieve the function of "optical switch". The electric field at a defect radius of r=0.29um is shown in the figure below. The incident light is half-transmissive and half-reflective, which is consistent with the conclusion obtained in the previous figure.

References