Preface
Bragg fiber is a type of air-core fiber that has received significant attention from researchers. It can allow light to propagate in the air core, which avoids problems caused by intrinsic material limitations such as absorption, dispersion, nonlinearity and low damage threshold. The FDE solver in this software can accurately calculate modes for complex structures, including photonic crystal(PC) Bragg fibers. In this example, we use the FDE solver to calculate the modes of the PC Bragg fiber described by Vienne et al [1] and further compare the results with those from Uranus et al [2].
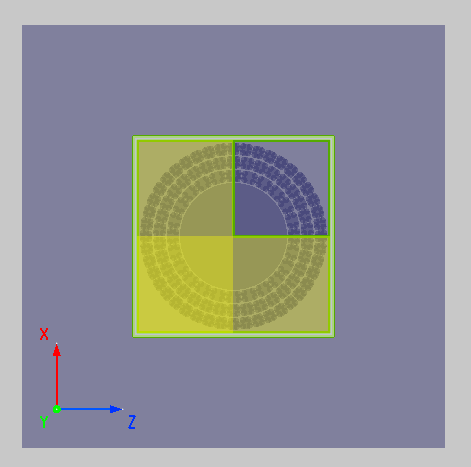
Simulation settings
Device Construction
The structure used in this example is the silica-air Bragg fiber described by Vienne et al. The fiber contains a complex microstructure in its middle. The microstructure is in diameter, with a air core in its center. The silica rings are separated by -thick air rings that comprise support bridges estimated to be only around thickness. A completed script for building this structure is available in the PC Bragg Fiber structure group in the project. Users can simply set the corresponding Variables in the structure group as required.
| Variable | Type | Value | Units |
|---|---|---|---|
| r_core | Length | 10 | microns(um) |
| t_annular | Length | 2.3 | microns(um) |
| t_ring | Length | 0.2 | microns(um) |
| t_bridge | Length | 0.045 | microns(um) |
| holes1 | Number | 24 | |
| holes2 | Number | 34 | |
| holes3 | Number | 44 | |
| y_span | Length | 0.3 | microns(um) |
Where r_core is the radius of the air core; t_annular is the thickness of the air ring; t_ring is the distance from the outer edge of the air core to the first silica ring; t_bridge is the thickness of the support bridge; holes1/2/3 are the number of air holes in the 1st/2nd/3rd layer.
Solver settings
As both the structure and the electromagnetic field are symmetric, the Symmetric and Anti-Symmetric boundary conditions can be used. The target modes require the electric field Ez be anti-symmetric parallel to the Z-direction and symmetric normal to the Z-direction, so we set the boundary conditions in the directions to be Anti-Symmetric. Employing symmetric and anti-symmetric boundary conditions can also reduce simulation time by eliminating unwanted modes that lack symmetry. The simulation employs a light with a wavelength at , consistent with the Reference[2:1]. From the results in the literature [2:2], it can be seen that the effective index of the target modes are both around 0.998, so the Guess Value can be set to 0.998 and the Total Mode can be set to 20, which can also reduce simulation time by eliminating unwanted modes.
Simulation results
Eigenmode
After the simulation, the target mode can be identified in the Modal List based on the electromagnetic field distribution. Among them, Mode#9 is the mode and Mode#10 is the mode, whose electric field distributions are shown below:
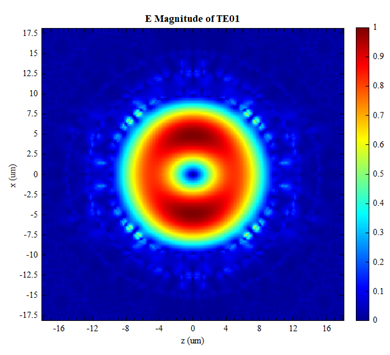
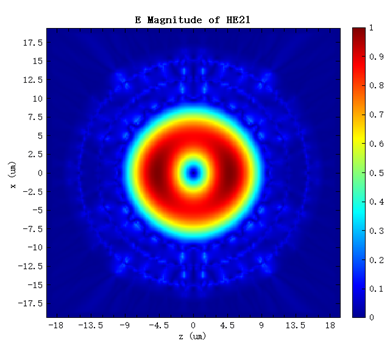
The following table shows the effective index and loss for the and modes, in comparison with the corresponding results from Uranus et al.
| - | neff TE01 | neff HE21 | Loss TE01 | Loss HE21 |
|---|---|---|---|---|
| Simulation | 0.997929 | 0.997860 | 0.575939 | 3.36613 |
| Uranus et al. | 0.99791 | 0.99785 | 0.015 | 0.14 |
The effective index calculated by this software is very close to the results from Uranus et al.
Convergence test
This type of structure is very sensitive to small changes in the numerical mesh (as well as real manufacturing imperfections), so a convergence testing is necessary. The number of mesh cells was refined from 200x200 to 800x800. The effective index of the mode and the mode at different numbers of mesh is plotted in the following figure.
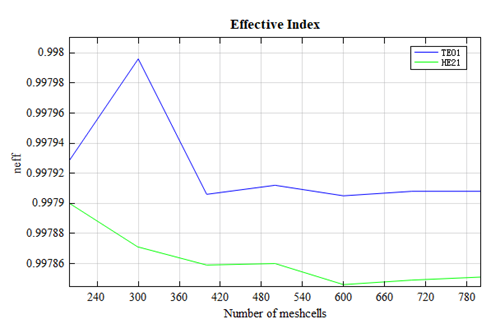
The effective index of the corresponding modes gradually converges as the number of mesh cells increases. At 800x800 cells, the effective index of the mode is 0.997908, and that of the mode is 0.997851. The results of the effective index approach to the results of Uranus et al.
Frequency analysis
Dispersion in fibers is the distortion of a signal that occurs when different frequency components propagate at different speeds. The effective index and dispersion of the mode were obtained by sweeping the frequency range from 240 THz to 280 THz. The results are shown below:
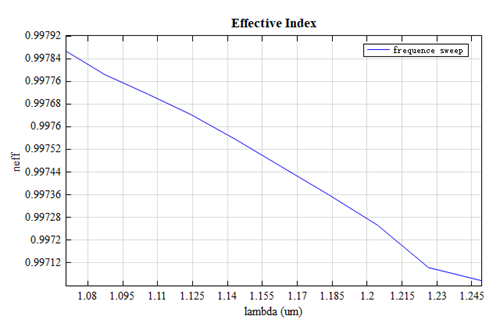
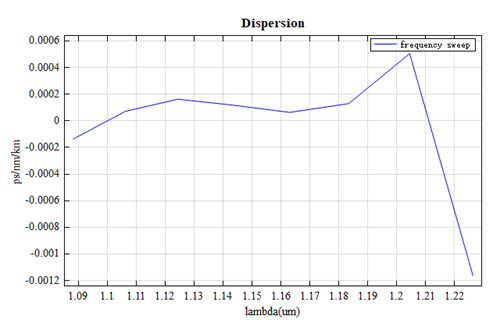
As the wavelength increases, the effective index decreases, which indicates the confinement for longer wavelength is weaker. From the above figure, we can see that this PC Bragg fiber can exhibit zero or negative dispersion under certain wavelength bands. Therefore, this air-core fiber with extremely low nonlinearity and high damage threshold enables high-speed, large-capacity and long-distance communication.
References
G. Vienne, Y. Xu, C. Jakobsen, H.J. Deyerl, T.P. Hansen, B.H. Larsen et al., "First demonstration of air-silica Bragg fiber," Post Deadline Paper PDP25, Optical Fiber Conference 2004, Los Angeles, 22-27 Feb. 2004. ↩︎
H. Uranus and H. Hoekstra, "Modelling of microstructured waveguides using a finite-element-based vectorial mode solver with transparent boundary conditions," Opt. Express 12, 2795-2809 (2004) ↩︎ ↩︎ ↩︎





