Preface

In conventional transmission line(TL), the phase velocity of the optical signal is less than the group velocity. As the optical signal propagates, its phase gradually lags. Antoniades et al. proposed a new type of negative refractive index(NRI) coplanar waveguide(CPW) TL^[1], which can be used after conventional TL for phase compensation, allowing the design frequency to propagate through all TLs to achieve positive, negative, or zero phase shifts. Compared to achieving a negative refractive index using thin wire strips and split-ring resonators, the propagation characteristics of this NRI metamaterial are mainly determined by lumped elements. Therefore this new NRI-TL can change the phase characteristics by simply adjusting the value of the lumped element instead of adjusting the length. Thus, this new NRI-TL offers significant advantages over conventional delay lines: its compact size, simplicity, ease of fabrication for planar microwave circuits, and linear phase response near the design frequency. This case study references $Antoniades'$ work and models a zero-phase-shift NRI-TL operating at a frequency of $f=1GHz$.

Simulation settings

Structure

The structure of the NRI-TL used in this case is shown in the figure below. This structure consists of a central conductor strip placed on a substrate and two semi-infinite conductor planes on either side. The central conductor strip acts as the signal transmission line, and the conductor planes on both sides act as the ground planes. The width of the central conductor strip is $w=4mm$, with a gap width of $g=0.1mm$ on both sides. The substrate has a height of $h=0.5mm$ and a relative permittivity of $\epsilon_r=2.2$.

On the central conductor strip, capacitors and inductors are periodically connected in series and parallel, as shown in the figure below. Each unit has a length of $d0=8mm$, with a series capacitor of $C0=12pF$ and two parallel inductors of $L0=50nH$. The capacitor shares the same width ($w$) as the signal line and has a length of $0.6mm$. The inductor has a length equal to the gap ($g$) and a width of $0.8mm$.

The thickness of the central conductor strip and the conductor planes can be neglected compared to the operating wavelength, so they can be simulated using 2D rectangles. According to the paper by Antoniades et al. ^[1:1], an optical signal with a frequency of $f=1GHz$ can achieve a 0° phase shift after passing through this structure.

Material

In the NRI-TL structure, the central conductor strip and the ground conductor planes can be simulated using Perfect Electrical Conductor (PEC), and the capacitor and inductor components can be modeled using RLC materials. RLC materials are used to specify lumped components with given resistance (R), inductance (L), and capacitance (C). When the two-dimensional structure selects the material as <RLC>, it can be defined in the material tab of the object, as shown in the figure below. <RLC> materials will not appear in the material library. It is important to note that the current flow direction for the capacitors is along the $Z$ axis, while the current flow direction for the inductors is along the $x$ axis.

Monitor

The figure below shows the simulation structure of 4-stage CPW units. The FDFP monitor T1 is located between the port source and the first CPW unit to measure the power injected by the port into the fundamental mode. The FDFP monitor T2 is placed behind the fourth CPW unit, with a distance of $4d_0=32mm$ from the T1 monitor. The T2 monitor is used to measure the power of the fundamental mode after the optical signal has passed through the CPW structure. Both T1 and T2 need to enable the mode expansion function, which can analyze the power ratio of any mode transmitted to the non-absorbing waveguide by calculating the overlap integral, for more details, please refer to the Mode Expansion.

Simulation results

Single Stage

After the simulation, the attached NRI_TL_phase_shifter.msf script can automatically calculate the phase shift of the optical signal after passing through the NRI-TL and compare it with the theoretical values as shown in the figure below. The theoretical calculation requires the effective permittivity $\epsilon_{eff}$ of the transmission line, which is obtained from the mode solved by the FDFP monitor: $\epsilon_{eff}=n_{eff}^{2}$.

The figure shows that the theoretical and the simulation results are very close. The theoretical zero phase shift occurs $f=0.985GHz$, while the simulated zero phase shift occurs $f=0.979GHz$, which indicates less than 3% difference from the design value of $1GHz$.

Multiple Stages

The attached script NRI_TL_phase_shifter_sweep.msf can automatically create and run three project files: a 1-stage CPW unit, 2-stage CPW units, and 4-stage CPW units. After the simulation, the script will also automatically calculate the phase shift results obtained for each project and generate a comparison graph of the simulation results against the theoretical results, as shown below.

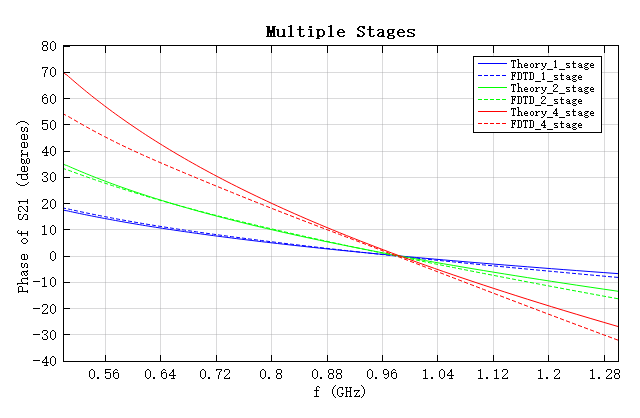
Obviously, as the number of CPW stages increases, the slope of the phase also increases, allowing for a larger phase shift. The zero phase shift frequency obtained from the simulation and the theoretical calculation are $f=0.979GHz$ and $f=0.985GHz$, respectively, with an error of less than 3%, and it is independent of the number of stages. This phenomenon is completely consistent with the conclusion in the paper ^[1:2].

References