Preface

The quality factor Q value is defined as the ratio of the center resonance wavelength to the full width at half maximum (FWHM) of the resonance peak. The higher the Q value, the better the wavelength selectivity of the device, the steeper the output peak, and the higher the sensitivity of the device. Generally, in the simulation of high-Q resonant cavities, the field amplitude obtained is inaccurate. The reason is that the loss rate in the high-Q resonant cavity is slow. If the simulation time is not long enough, the field in the cavity will not decay to 0 at the end of the simulation. At this time, the amplitude of the mode field in the cavity needs to be corrected to obtain the final actual amplitude. This case constructs a photonic crystal resonant cavity structure to demonstrate how to correct the field amplitude when the simulation time of a high-Q resonant cavity is insufficient.

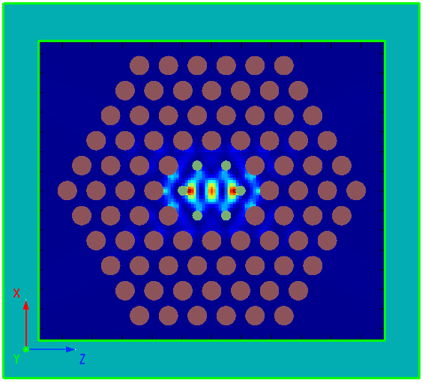
Simulation Setting

Device construction

The resonant cavity used in this case is a tantalum oxide ($Ta_{2}O_{5}$) with hexagonal lattice air holes. In the simulation of photonic crystal structures, mesh partitioning is very important, and you must be sure to use the same mesh partitioning method for each periodic structural cell. In this case, a uniform override mesh is added to ensure the correct distribution of periodic cells. Due to the symmetry of the structure and the source, the Symmetric boundary conditions are used in the $X_{min}$ and $Z_{min}$ directions, and the Anti-Symmetric boundary conditions are used in the $Y_{min}$ direction. The symmetric/anti-symmetric boundary conditions can be used to reduce the simulation region to 1/8, thus reducing the memory required for simulation.

Correcting field amplitudes

The absolute mode field describes the spatial shape of the mode field and the coupling strength between a source and a cavity mode. Since the source used in FDTD does not represent the actual source used to excite the cavity, the absolute mode field is usually not a variable worth paying attention to. The quality factor Q and the relative mode field distribution are usually what we are interested in. However, if the source you are using in FDTD is the source that actually excites the cavity, you may want to know the actual amplitude of the mode field. As shown in the figure below, the reason for the inaccurate mode amplitudes of high-Q cavities is that the simulation ends before the cavity field decays to 0, and the calculated fields from FDFP frequency monitors are only correct when the entire time signal is taken into account.

You can correct the amplitude of the absolute field by scaling in/out the amplitude of the simulated original field. The field amplitude is proportional to the area under the curve in the figure above, so you can correct the amplitude according to the proportion of the area corresponding to the simulation time. The scale factor of the field amplitude is determined by the resonant frequency $\omega$, the simulation end time $t_{end}$ and the mode quality factor $Q$, and can be expressed by the following formula.

$\gamma=\frac{1}{1-e^{\frac{-\omega t_{end}}{2Q}}}$

$\vec{E}=\gamma\vec{E}_{simulation}$

Therefore, we only need to use high Q analysis group to calculate the Q value of the cavity to obtain the scaling ratio of the original field amplitude, thereby correcting the absolute field amplitude.

Simulation Results

Run the script file in the attachment to automatically run two simulations with simulation times of 500fs and 3000fs. The figure below shows the electric intensities obtained by the time monitors in the two simulations change over simulation time. It can be seen that when the simulation time of 500fs is not enough for the field to completely decay, the final field amplitude is inaccurate and needs to be corrected to compensate for the shorter simulation time.

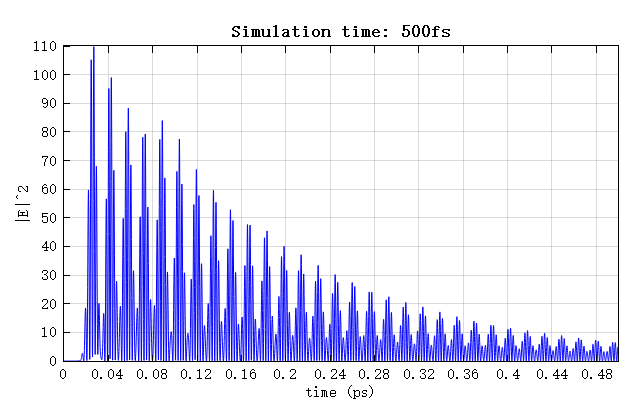
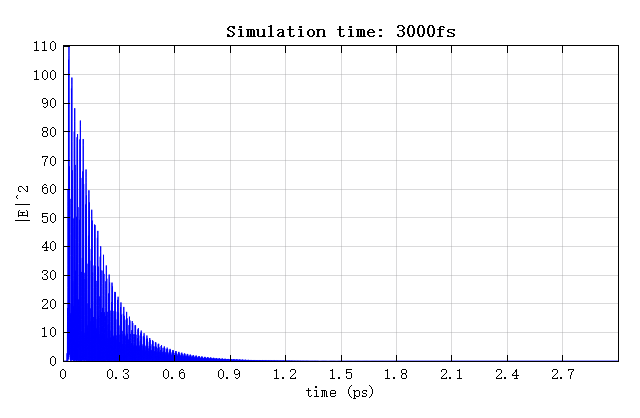
The figure below shows the original field distribution in the resonant cavity obtained from the FDFP monitor. Note that the field amplitude inside the cavity depends on the simulation time. If the simulation time is not long enough, the field amplitude will be smaller than it should be. The figure clearly indicates that when the simulation time is 500fs, the field amplitude is significantly smaller than that when the simulation time is 3000fs.

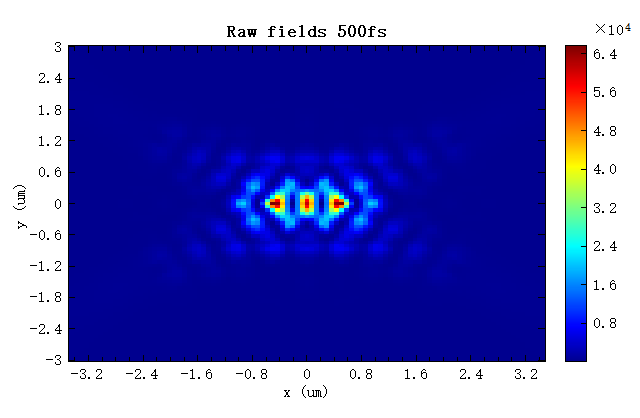
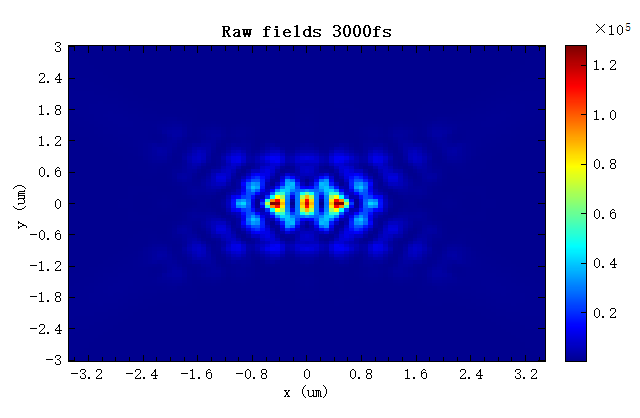
The figure below shows the electric intensity distributions after amplitude corrections that are obtained at simulation times of 500fs and 3000fs. The field amplitudes obtained at different simulation time are basically consistent after correction. It can be seen that the field simulated at 500fs is amplified to compensate for the shortened simulation time. The field scale factor obtained at the simulation time of 3000fs is approximately equal to 1. If the simulation runs long enough for the field to decay completely, the field need not be rescaled and the scale factor should be equal to 1.

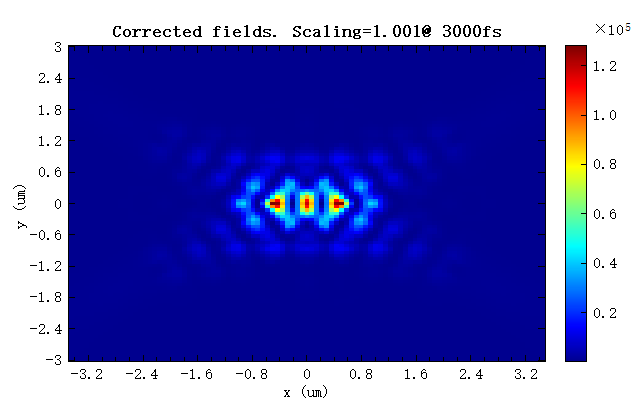
Note that although the simulation time is different, the calculated Q value is the same because the field distribution obtained in the two simulations is the same. Therefore, the simulation can end in a short time, with no need to end after the field has completely decayed. All information can be obtained from shorter simulations by amplitude corrections.