Preface

A Bragg grating is an optical device in which there is a periodic variation in the effective refractive index of the structure. The waveguide Bragg grating is a type of one-dimensional photonic crystal structure that enables wavelength selection through periodic modulation of the refractive index. This property can be used to create various optical filters. The impact of the geometrical parameters of the sidewall corrugation, such as depth or misalignment, on the performance of Bragg gratings can be analyzed in silicon waveguide Bragg gratings, as demonstrated by Wang et al.

Simulation settings

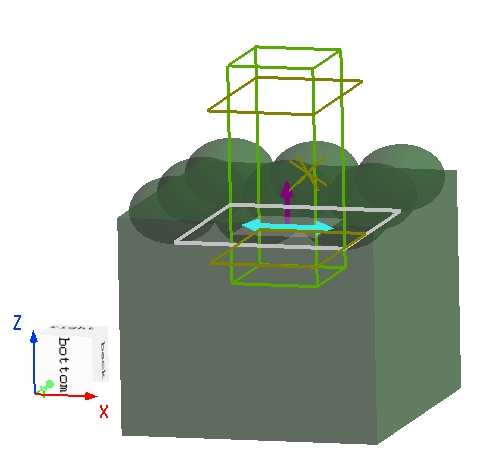
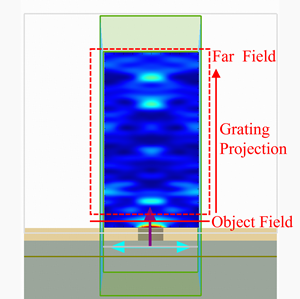
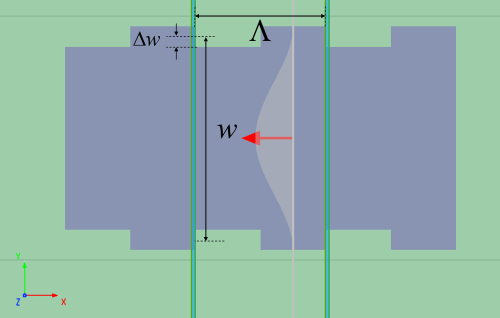
This example is simulated by 3D FDTD. A Bragg grating is composed of a silicon grating device placed on an insulating silicon substrate. The structure is detailed in the figure below. To simulate an infinite-period grating by just a single grating cycle, a 'Bloch' boundary condition is set in the x-direction. The table below shows the structural parameters in this figure. $\Lambda$ represents the cell length of a single cycle of the Bragg grating, $w$ represents the average width of the waveguide, and $\Delta w$ represents the depth of the grating corrugation.

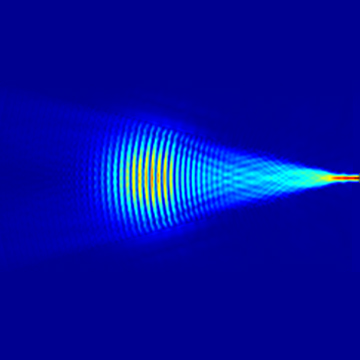
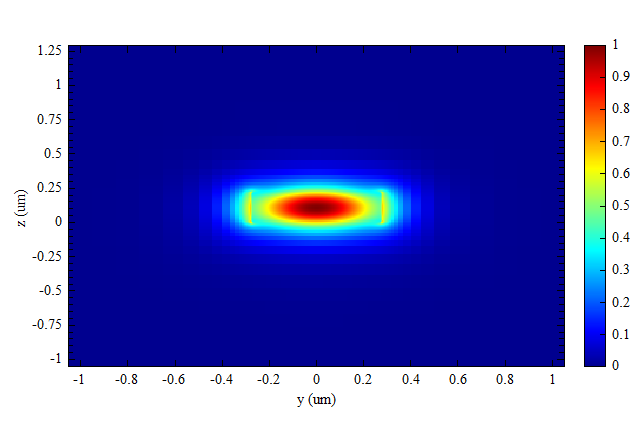
In this example, the light source is set to be a mode light source. The fundamental mode TE0 field is shown below.

Material

• substrate
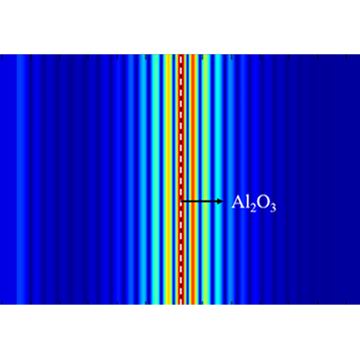
  The substrate material used in this example is SiO2 (Glass) - Palik from the software's built-in material library. The wavelength range of the light source is $1.52\mu m$ to $1.56\mu m$. As shown in the below figure, the refractive indices of SiO2 after the fitting are 1.44415 in the real part and 0 in the imaginary part in the wavelength range.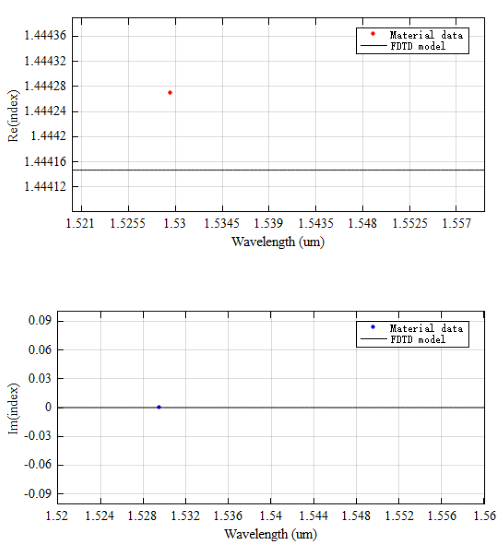

• grating
  The grating material used in this example is a silicon material based on the Lorentz model. For specific details on the setup of the Lorentz model, please refer to Drude_Debye_Lorentz.

$\varepsilon_{total}(f) =\varepsilon + \frac{\varepsilon_p.\omega_p^2}{\omega_p^2+4\pi j\gamma_p.f-(2\pi f)^2}$

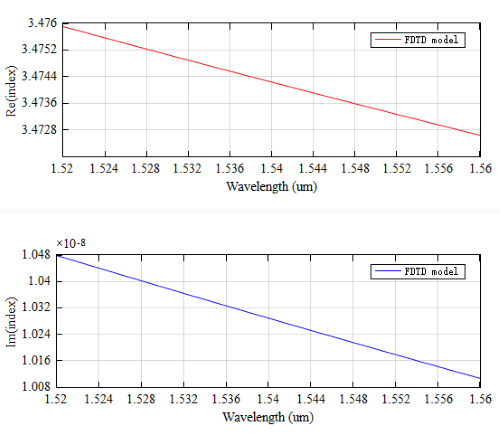
In this example, $\varepsilon = 7.98737$, $\varepsilon_p = 3.68799$, $\omega_p = 3.93282e+15$, $\gamma_p = 1e+8$, the figure below displays the real and imaginary parts of the refractive index of the Si material after this setting.

Simulation results

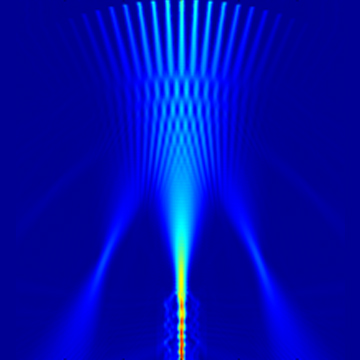
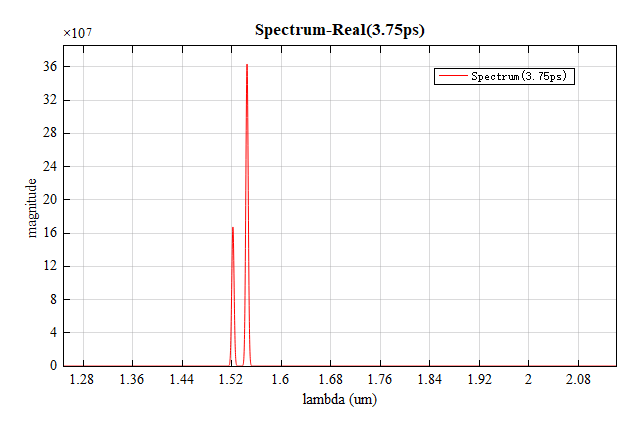
In this example, the bandstructure analysis group calculates the spectrum of Bragg grating. After the run, this analysis group will get the spectrum of the grating at the wave vector $k_x=\pi/\Lambda$. Open the appendix script file and run it directly. In the band structure result, you can be able to obtain the energy band spectrum of the Bragg grating when the corrugation depth is 0.05$\mu$m, as shown below.

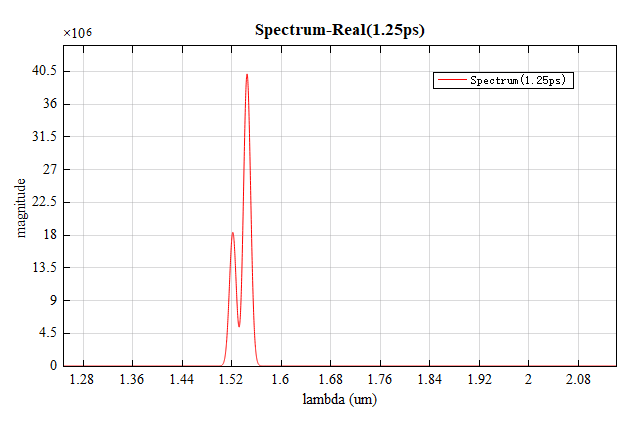
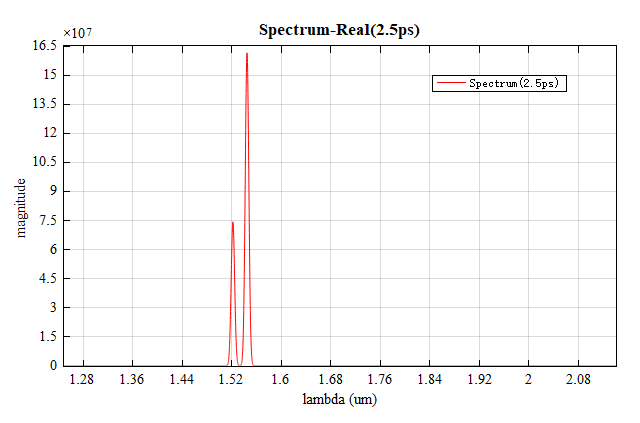
It is worth noting that the width of the resonance peaks in the spectrum is closely related to the calculation time. As the calculation time increases, the resonance becomes stronger and its peak becomes sharper. For gratings with shallow sidewall corrugation, additional calculation time is required to distinguish different resonance peaks in the spectrum. The initial time is set to $1.25ps$ in this example. Gradually increasing the computation time reduces the width of the resonance peaks, as shown in the following figures, where the computation time is $2.5ps$ for the above figure and $3.75ps$ for the below figure.

Parameter analyses

The size of the bandwidth can be calculated from the wavelengths of the two resonance peaks in the spectrum. Furthermore, we can utilize the size of the bandwidth to analyze the performance of the grating. The interaction between the optical modes in the grating and the grating is typically described by the coupling coefficient $\kappa$, expressed as follows:

$\kappa=\pi n_g\Delta\lambda/\lambda_0^2$

where $\kappa$ is the grating coupling coefficient, $\Delta\lambda$ is the bandwidth, $\lambda_0$ is the center wavelength and $n_g$ is the group refractive index at the central wavelength.

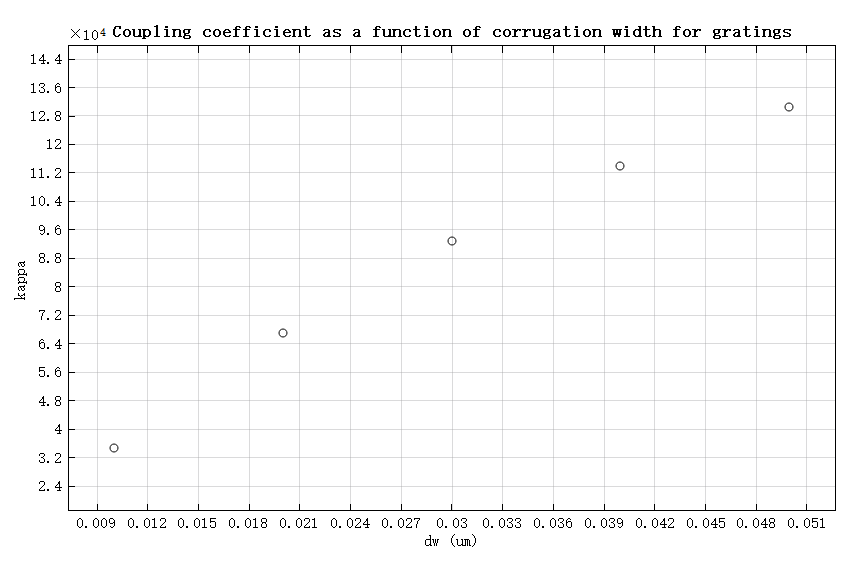
The impact of corrugation width on grating performance

When scanning with $\Delta w$ ranging from $0.01\mu m$ to $0.05\mu m$, it is possible to observe the effect of grating depth on grating performance (the coupling coefficient $\kappa$). By opening the appendix project and running the parameter sweep, you can obtain the trend of grating performance with corrugation depth. The scatter plot of $\kappa$ is depicted below, which is similar to the one in reference ^[1] Figure 7.

References