Preface

Woodpile-Lattice photonic crystals are generally composed of a stack of cuboid dielectric materials arranged alternately vertically. In this case, the Woodpile-Lattice photonic crystal device is constructed based on the reference^[1], and the FDTD solver is used to explore the energy bandstructure of the photonic crystal.

Simulation settings

Device introduction

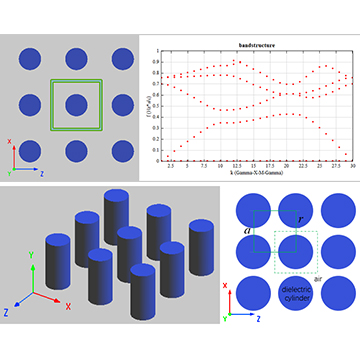
The FDTD solver is used to analyze the bandstructure of a woodpile-lattice structure consisting of homogeneous dielectric prisms arranged periodically. The parallel and vertical staggered stacking of infinite dielectric prisms realize the periodic distribution of refractive index and thus form the photonic bandgap^[2]. In this example, the complete bandgap is generated by dielectric prisms with a refractive index of 3.47851 in the air environment. See Reference^[1:1] for details on the structure of the woodpile, the Brillouin zone of the woodpile-lattice, and the coordinates of the special points in this case.

Device construction

The construction and simulation settings for this case are similar to the case Bandstructure of 2D square lattice. The attachment woodpile.mpps is the project file for this case. Open the file to view the detailed parameter settings. Users can directly select and insert a woodpile structure from the built-in structure group library. In order to satisfy the periodic boundary conditions, two periodic units must be included in the simulation region of the FDTD. Therefore, matching dipole sources are created within two periodic cells to avoid the problem of artificial region folding. For a similar problem, see Triangular lattice photonic crystal.

Simulation results

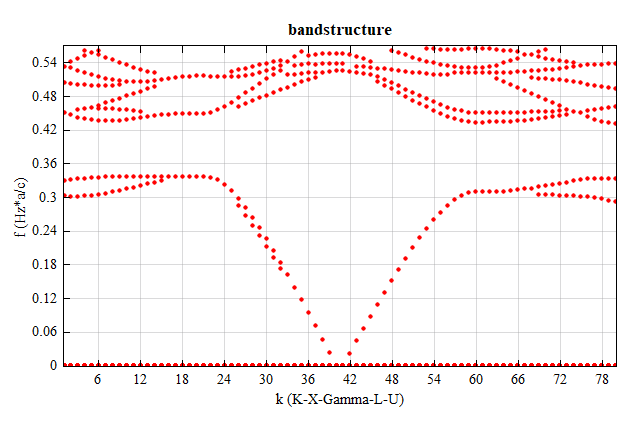
Download and open the attachment woodpile.mpps and run all the parameter sweeps. After running all the parameter sweeps, download and run the script woodpile.msf to obtain the sweep results and draw the bandstructure diagram, as shown below.

References

"Photonic Crystal Laser-Driven Accelerator Structures", A dissertation submitted to the department of physics and the committee on graduate studies of Stanford University in partial fulfillment of the requirements for the degree of Doctor of Philosophy, Benjamin Cowan, March 2007 - Chapter 3. ↩︎ ↩︎
Ho K M , Chan C T , Soukoulis C M , et al. Photonic band gaps in three dimensions: New layer-by-layer periodic structures[J]. Solid State Communications, 1994, 89(5):413-416. ↩︎

Recommend

Photonic Crystal Optical Switch Using Line Defects

The self-collimation(SC) effect of photonic crystals(PCs) achieves collimated radiation with almost no diffraction effect when the incident light propagates along a particular direction of the crystal. Line defects in 2D PCs cause bending and splitting of the SC beam. In this example, the effect of "optical switching" can be achieved by altering the line defects (radius of the dielectric rod) in the photonic crystal.

Bandstructure of 2D Square Lattice

Photonic crystals, as a dielectric structure with periodic changes in dielectric constant, can prevent light of a specific frequency from propagating internally, forming a photonic band gap.

Bandstructure of 2D Triangular Lattice

In this case, a 2D triangular-lattice PC formed by air cylinders arranged in parallel in the medium is constructed, and its bandstructure is calculated.

Bandstructure of 3D Cubic Lattice

3D Cubic Lattice is a special case of 3D Rectangular Lattice. The lattice spacing of this type of photonic crystal is equal in three axes in space.

Bandstructure of BCC Lattice and FCC Lattice

In this case, BCC and FCC photonic crystals are constructed and their bandstructures are analyzed using FDTD solvers.

Bandstructure of a Magneto-Optical Waveguide

In this case, the optical waveguide model with periodic structure in the propagation axis is constructed, and the bandstructure of the waveguide is analyzed.

Correcting Field Amplitudes for High-Q Cavities

Generally, in the simulation of high-Q resonant cavities, the field amplitude obtained is inaccurate. The reason is that the loss rate in the high-Q resonant cavity is slow. If the simulation time is not long enough, the field in the cavity will not decay to 0 at the end of the simulation. At this time, the amplitude of the mode field in the cavity needs to be corrected to obtain the final actual amplitude. This case constructs a photonic crystal resonant cavity structure to demonstrate how to correct the field amplitude when the simulation time of a high-Q resonant cavity is insufficient.

2D-Periodic Metallic Photonic Crystal Slabs

The ability to modify an object's thermal radiation profile is important in many areas of applied physics and engineering. It has been noted that periodic engineering of devices made of metallic and dielectric materials at the subwavelength scale can change the thermal radiation properties of the device. This case studies the thermal radiation of a photonic crystal obtained by periodically arranging a device made of metallic tungsten and a dielectric material.

Organic Solar Cell with PC Structure

How to improve Organic solar cells'(OSCs) photoelectric conversion efficiency (PCE) is an urgent problem to be solved. One of the more commonly used methods is to add micro-nano structures for light trapping into the photoactive layer of OSCs to increase light absorption, thereby improving PCE. The photonic crystal (PC) structure is used in the photoactive layer of OSCs, which can enhance the light absorption of solar cells in specific wavelength bands. This case uses FDTD simulation to analyze the light absorption of an OSC with a 2D hexagonal-lattice PC structure.

Exciting the Surface Plasmon-Polaritons in Graphene

The chemical potential of graphene can be regulated by methods such as voltage or chemical doping. This property makes graphene highly versatile in the field of material-light interactions, particularly in relation to surface plasmon polaritons (SPPs). By exciting surface plasmons, graphene significantly enhances its ability to interact with light.