Preface

Body-Center Cubic Lattice (BCC) and Face-Center Cubic Lattice (FCC) are two common types of 3D photonic crystal structures. In this case, BCC and FCC photonic crystals are constructed and their bandstructures are analyzed using FDTD solvers.

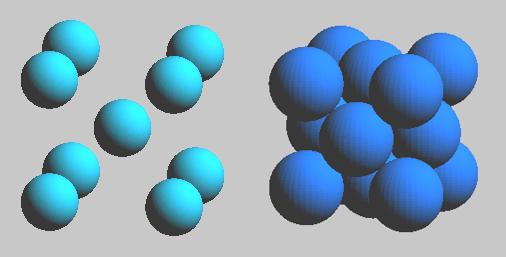
Simulation settings

Device introduction

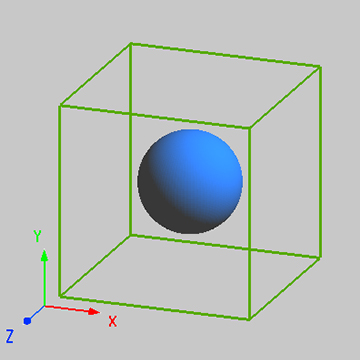
In this case, the FDTD solver is used to analyze the bandstructure of a photonic crystal composed of homogeneous dielectric spheres arranged according to two lattice structures, FCC and BCC. These two kinds of lattice structures belong to the cubic crystal system, but their minimum periodic structural elements are not rectangular structures, so they do not conform to the FDTD rectangular mesh algorithm. Therefore, different from the simulation settings of Bandstructure of 3D Cubic Lattice, special settings should be made for the simulation object based on the lattice type.

Device construction

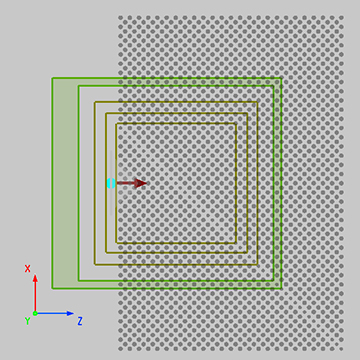
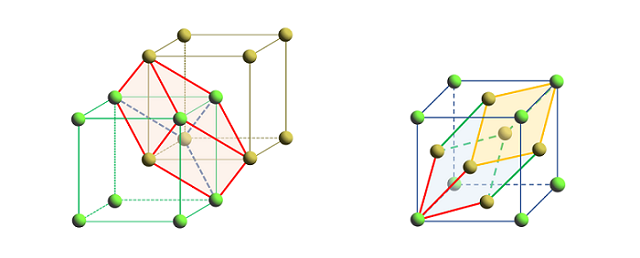
The construction and simulation Settings of the photonic crystal in this case are similar to the case Bandstructure of 2D Square Lattice, which will not be repeated here. Please download the attached project file to view the detailed information of the case. Both BCC and FCC lattices belong to the cubic crystal system, and their unit cell shapes are cubic, which meets the basic requirements of the FDTD solver for the rectangular simulation region. Therefore, the simulation region is set to be consistent with the space range of the simplest unit cell structure, and the region boundary is set to the Bloch periodic boundary condition. The primitive cell structure in the BCC and FCC lattices is shown in the figure below. Similar to the triangular lattice, it is obvious that its minimal periodic structure is non-rectangular. There are multiple primitive cell structures in the simulation region, and at least four primitive cell units in the simulation region of FCC lattice photonic crystal. Likewise, to avoid the problem of artificial region folding, add matching dipole sources in each primitive cell, see case Bandstructure of 2D Triangular Lattice for more information. In addition, when generating the mesh in the FCC lattice simulation area, it is necessary to ensure that the mesh cells are uniformly and symmetricly distributed about the central coordinate axis, and the number of mesh cells in each axis can be divisible by 4. Thus, the meshes of each sphere structure are same, and the periodicity of the index distribution in the simulation region is realized. See the corresponding simulation in the attachment for details.

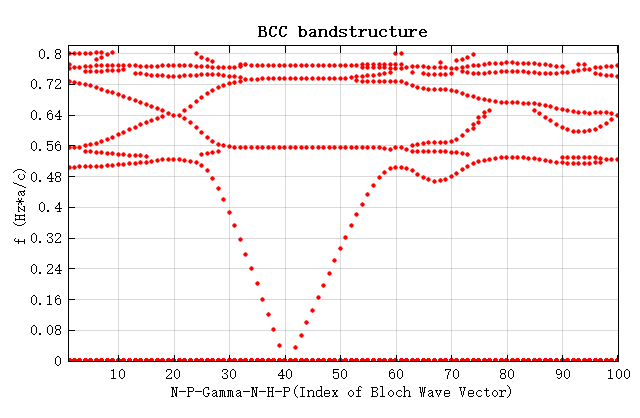
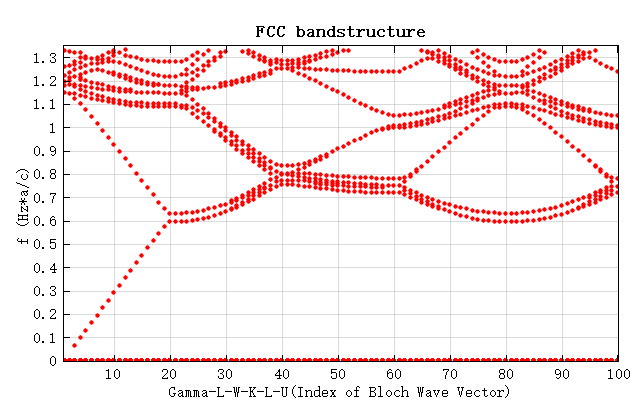
Simulation results

Attachments contain project files for BCC- and FCC- lattice photonic crystal. Download and open the project files respectively. After running all the parameter sweeps, run the corresponding scripts to obtain the parameter sweep results and draw the bandstructure diagram, as shown in the following figure.

Recommend

Photonic Crystal Optical Switch Using Line Defects

The self-collimation(SC) effect of photonic crystals(PCs) achieves collimated radiation with almost no diffraction effect when the incident light propagates along a particular direction of the crystal. Line defects in 2D PCs cause bending and splitting of the SC beam. In this example, the effect of "optical switching" can be achieved by altering the line defects (radius of the dielectric rod) in the photonic crystal.

Bandstructure of 2D Square Lattice

Photonic crystals, as a dielectric structure with periodic changes in dielectric constant, can prevent light of a specific frequency from propagating internally, forming a photonic band gap.

Bandstructure of 2D Triangular Lattice

In this case, a 2D triangular-lattice PC formed by air cylinders arranged in parallel in the medium is constructed, and its bandstructure is calculated.

Bandstructure of 3D Cubic Lattice

3D Cubic Lattice is a special case of 3D Rectangular Lattice. The lattice spacing of this type of photonic crystal is equal in three axes in space.

Bandstructure of a Magneto-Optical Waveguide

In this case, the optical waveguide model with periodic structure in the propagation axis is constructed, and the bandstructure of the waveguide is analyzed.

Correcting Field Amplitudes for High-Q Cavities

Generally, in the simulation of high-Q resonant cavities, the field amplitude obtained is inaccurate. The reason is that the loss rate in the high-Q resonant cavity is slow. If the simulation time is not long enough, the field in the cavity will not decay to 0 at the end of the simulation. At this time, the amplitude of the mode field in the cavity needs to be corrected to obtain the final actual amplitude. This case constructs a photonic crystal resonant cavity structure to demonstrate how to correct the field amplitude when the simulation time of a high-Q resonant cavity is insufficient.

2D-Periodic Metallic Photonic Crystal Slabs

The ability to modify an object's thermal radiation profile is important in many areas of applied physics and engineering. It has been noted that periodic engineering of devices made of metallic and dielectric materials at the subwavelength scale can change the thermal radiation properties of the device. This case studies the thermal radiation of a photonic crystal obtained by periodically arranging a device made of metallic tungsten and a dielectric material.

Organic Solar Cell with PC Structure

How to improve Organic solar cells'(OSCs) photoelectric conversion efficiency (PCE) is an urgent problem to be solved. One of the more commonly used methods is to add micro-nano structures for light trapping into the photoactive layer of OSCs to increase light absorption, thereby improving PCE. The photonic crystal (PC) structure is used in the photoactive layer of OSCs, which can enhance the light absorption of solar cells in specific wavelength bands. This case uses FDTD simulation to analyze the light absorption of an OSC with a 2D hexagonal-lattice PC structure.

Exciting the Surface Plasmon-Polaritons in Graphene

The chemical potential of graphene can be regulated by methods such as voltage or chemical doping. This property makes graphene highly versatile in the field of material-light interactions, particularly in relation to surface plasmon polaritons (SPPs). By exciting surface plasmons, graphene significantly enhances its ability to interact with light.

Bandstructure of Woodpile Lattice

In this case, the Woodpile-Lattice photonic crystal is constructed, and the FDTD solver is used to explore the energy bandstructure of the photonic crystal.