Preface

The FDE solver is used to solve modes for the waveguide whose structure is periodic in the propagation direction. However, for structures composed of anisotropic materials or other nonlinear materials, we can solve the dispersion or bandstructure by the FDTD solver. In this case, the optical waveguide model with periodic structure in the propagation axis is constructed, and the bandstructure of the waveguide composed of isotropic material and diagonal anisotropic material is analyzed respectively.

Simulation settings

Device introduction

The FDTD solver is used in this case to analyze the bandstructure of an optical waveguide consisting of isotropic and anisotropic materials. Unlike the isotropic material, the dielectric constant of the anisotropic material is not equal in all directions, which will break the degeneracy between the modes and the calculated band structure will change significantly. The straight waveguide extends infinitely in the propagation axis, and its structure can be considered periodic. Therefore, periodic boundary conditions with only one cell in the simulation area are used in z-axis.

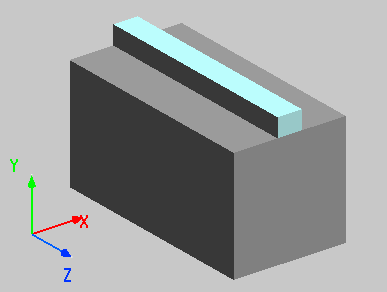
The refractive index of the isotropic waveguide core in this model is 1.5. As shown in the figure, the straight waveguide has a width $w$ of 2.6 μm and a height $h$ of 2 μm, extending infinitely along the z-axis. Dielectric materials with a refractive index of 1.4 were selected for the waveguide substrate.

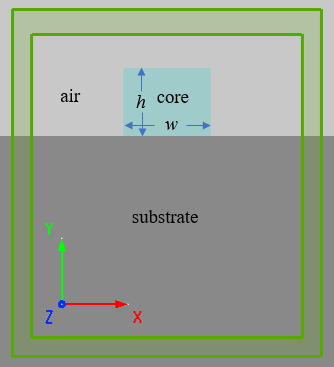
Device construction

Detailed information such as the object of the simulation model can be found in the attached project file nr_waveguide3d.mpps. In general, in order to calculate the complete bandstructure of the target structure, the dipole array is used as the input source that is set to the target frequency range. All the above-mentioned notices have been detailed in the bandstructure-related case. (See Bandstructure of 2D Square Lattice for a detailed example of bandstructure simulation.) However, for this case, our goal is to find the influence of the waveguide material on the mode, and we only observe how the bandstructure changes with the adjustment of the waveguide system, so we use the mode source here instead of the dipole array. The mode source can solve the incident pattern, which converges more quickly. It can be found that the waveguide in this case supports two modes of TM and TE. Since these two modes are orthogonal, we construct two mode sources to inject two modes of TE and TM respectively, and solve these two modes in the wavelength range of 1.5 μm to 1.6 μm.

Simulation results

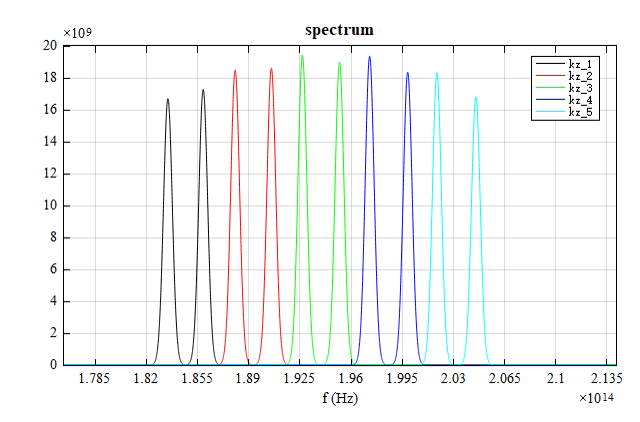
The attachment nr_waveguide3d.mpps is the project file for this case. After downloading, the resonance spectrum under a specific wave vector can be obtained. Parameter sweeps were run to obtain the resonance spectrum at different wave vectors $k$ . To speed up the operation, only five points are selected from the range $k_z = 5.6e ^{6}$ ~ $6.2e^{6} rad/m$ . Running the parameter sweep can calculate the resonance spectrum at five different wave vectors. Once you're done, load and run the nr_waveguide3d.msf file to calculate the effective refractive index and propagation constant.

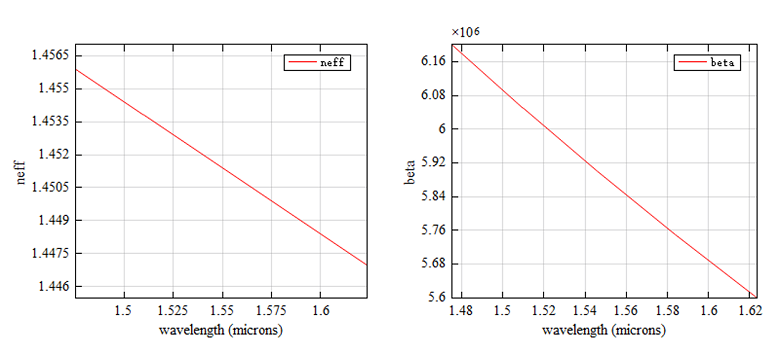
First, we simulate a regular waveguide composed of isotropic materials. The material of the waveguide core is set to a dielectric material with a refractive index of 1.5. After running the parameter sweep, open the nr_waveguide3d.msf file and run it. The effective refractive index can be calculated as $k/k_0$ , where $k_0$ is the wave number in vacuum. The final figures such as effective refractive index vs wavelength, propagation constant vs wavelength are shown as follows:

The resonance spectrum at different wave vectors is shown below. Clearly, the mode degeneracy results in only one resonance peak per wave vector $k$ in an isotropic waveguide.

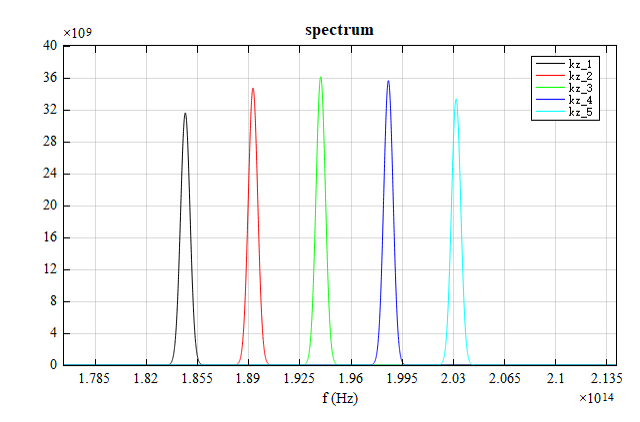
Next, the calculation of anisotropic material waveguides is performed. Click Materials in the main interface of the software to enter the Material Library window. Click "Go to Project Material Library" in the Material List to enter the project material library page. Double-click the material "core" to enter the editing interface of the material, check Anisotropy (Diagonal) here, and use diagonal anisotropic material. As shown in the figure, the refractive indices $xx$ , $yy$ and $zz$ of the diagonal anisotropic material are entered into the corresponding input box as 1.49, 1.51 and 1.50, respectively.

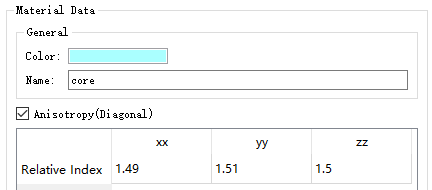
Re-running the simulation, the spectrum of the anisotropic waveguide at a particular wave vector can be obtained. After running the parameter sweep again, run the attached script to view the calculation results of the anisotropic waveguide. As shown below, there are obvious differences in the effective refractive index and propagation constant corresponding to the two different modes.

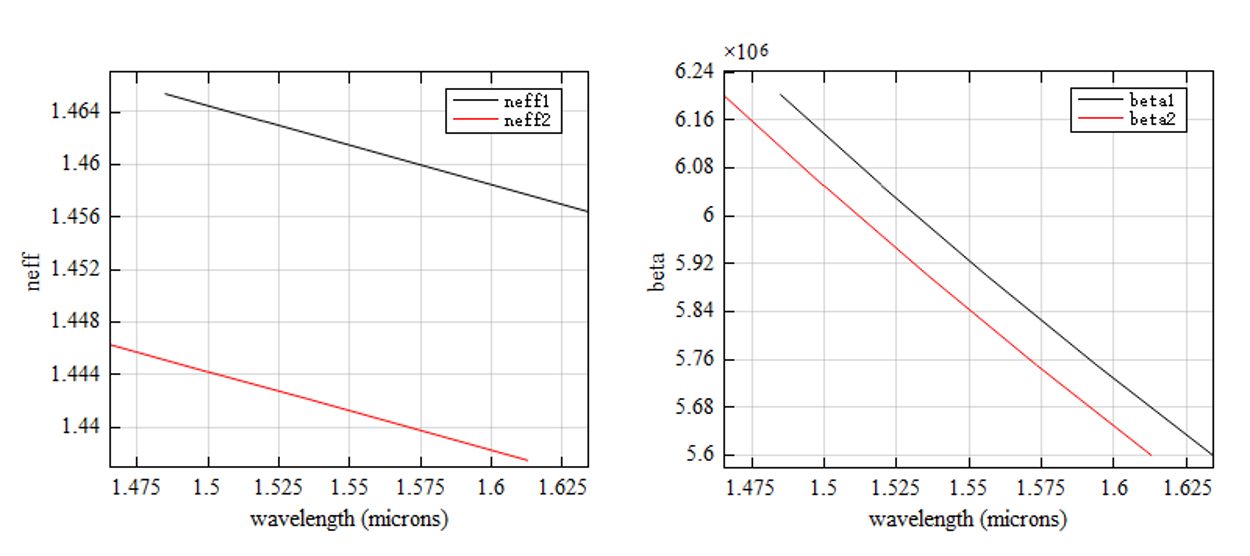
The time monitor at the center of the waveguide records the variation of the electric field signal in the waveguide with time. The amplitudes of $E_x$ and $E_y$ are shown in the figure below. It can be seen that there is no coupling between the two modes, which is because the two modes are orthogonal to each other.

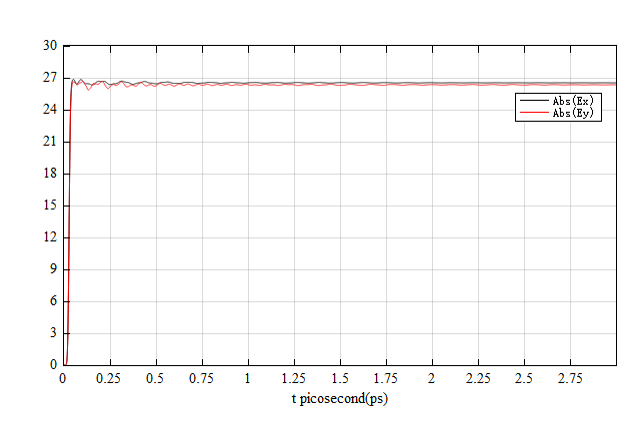
As you can see in the figure below, instead of a single peak at each $k$ in the spectrum, there are now two resonance peaks. It indicates that there are two resonant frequencies corresponding to the two modes. This is due to the breaking of the degeneracy of TM and TE modes in the isotropic model.

Recommend

Photonic Crystal Optical Switch Using Line Defects

The self-collimation(SC) effect of photonic crystals(PCs) achieves collimated radiation with almost no diffraction effect when the incident light propagates along a particular direction of the crystal. Line defects in 2D PCs cause bending and splitting of the SC beam. In this example, the effect of "optical switching" can be achieved by altering the line defects (radius of the dielectric rod) in the photonic crystal.

Bandstructure of 2D Square Lattice

Photonic crystals, as a dielectric structure with periodic changes in dielectric constant, can prevent light of a specific frequency from propagating internally, forming a photonic band gap.

Bandstructure of 2D Triangular Lattice

In this case, a 2D triangular-lattice PC formed by air cylinders arranged in parallel in the medium is constructed, and its bandstructure is calculated.

Bandstructure of 3D Cubic Lattice

3D Cubic Lattice is a special case of 3D Rectangular Lattice. The lattice spacing of this type of photonic crystal is equal in three axes in space.

Bandstructure of BCC Lattice and FCC Lattice

In this case, BCC and FCC photonic crystals are constructed and their bandstructures are analyzed using FDTD solvers.

Correcting Field Amplitudes for High-Q Cavities

Generally, in the simulation of high-Q resonant cavities, the field amplitude obtained is inaccurate. The reason is that the loss rate in the high-Q resonant cavity is slow. If the simulation time is not long enough, the field in the cavity will not decay to 0 at the end of the simulation. At this time, the amplitude of the mode field in the cavity needs to be corrected to obtain the final actual amplitude. This case constructs a photonic crystal resonant cavity structure to demonstrate how to correct the field amplitude when the simulation time of a high-Q resonant cavity is insufficient.

2D-Periodic Metallic Photonic Crystal Slabs

The ability to modify an object's thermal radiation profile is important in many areas of applied physics and engineering. It has been noted that periodic engineering of devices made of metallic and dielectric materials at the subwavelength scale can change the thermal radiation properties of the device. This case studies the thermal radiation of a photonic crystal obtained by periodically arranging a device made of metallic tungsten and a dielectric material.

Organic Solar Cell with PC Structure

How to improve Organic solar cells'(OSCs) photoelectric conversion efficiency (PCE) is an urgent problem to be solved. One of the more commonly used methods is to add micro-nano structures for light trapping into the photoactive layer of OSCs to increase light absorption, thereby improving PCE. The photonic crystal (PC) structure is used in the photoactive layer of OSCs, which can enhance the light absorption of solar cells in specific wavelength bands. This case uses FDTD simulation to analyze the light absorption of an OSC with a 2D hexagonal-lattice PC structure.

Exciting the Surface Plasmon-Polaritons in Graphene

The chemical potential of graphene can be regulated by methods such as voltage or chemical doping. This property makes graphene highly versatile in the field of material-light interactions, particularly in relation to surface plasmon polaritons (SPPs). By exciting surface plasmons, graphene significantly enhances its ability to interact with light.

Bandstructure of Woodpile Lattice

In this case, the Woodpile-Lattice photonic crystal is constructed, and the FDTD solver is used to explore the energy bandstructure of the photonic crystal.