Preface

3D Cubic Lattice is a special case of 3D Rectangular Lattice. The lattice spacing of this type of photonic crystal is equal in three axes in space. In this case, the 3D cubic-lattice photonic crystal is constructed, and the FDTD solver is used to simulate the bandstructure of the dielectric sphere 3D cubic-lattice photonic crystal.

Simulation settings

Device introduction

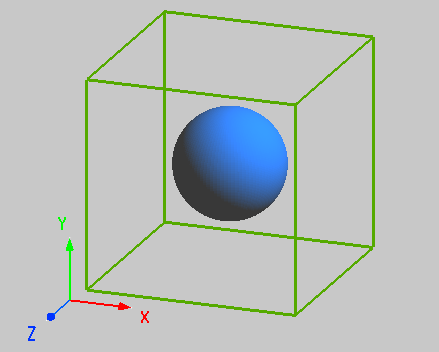
The FDTD solver is used to analyze the bandstructure of a cubic-lattice photonic crystal consisting of a periodic arrangement of spheres in a homogeneous medium. Similar to the 2D square-lattice photonic crystal, the periodic arrangement of the dielectric spheres in air realizes a periodically varying refractive index distribution in space, forming a photonic bandgap. In this example, the radius $R$ of the periodically arranged dielectric sphere is 0.13 μm, the refractive index of the dielectric material is 3.00, the background is air, and the lattice spacing $a$ of the cubic lattice is 0.5 μm.

Device construction

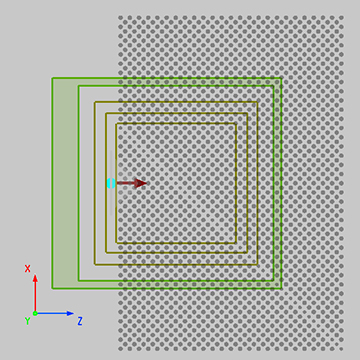
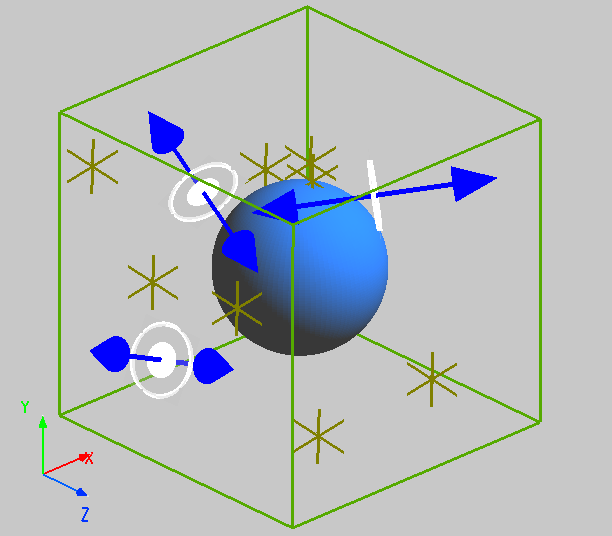
The simulation settings of this case are similar to the Bandstructure of 2D Square Lattice case. The attachment 3D_cubic.mpps is the demonstration file. After opening the project file, you can see the detailed parameters and settings. The 3D cubic lattice structure changes periodically in space in all three axes, which requires the use of 3D FDTD simulation. By adjusting the coordinates of the geometric center and the axial range of the FDTD, the simulation area is set to be the same as the periodic unit of the 3D cubic lattice, and the structural unit is located in the center of the simulation area, as shown in the following figure. In order to make the structural unit exhibit periodic distribution, Bloch boundary conditions are used along z, x and y axes. The analysis group 'Dipole Clouds' and 'bandstructure' are used to create a fixed number of dipole sources and time monitors at random locations in the 3D FDTD simulation region. Note that the variable of lattice type is changed to 3(3D rectangular lattice) in the analysis group 'Dipole Clouds'.

Simulation results

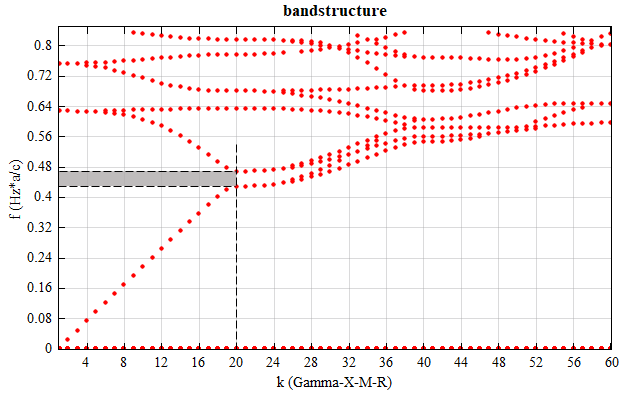
Download and open the attachment 3D_cubic.mpps and run all parameter sweeps manually. After completing the parameter sweep of the wave vector, download the script file 3D_cubic.msf for calculating the corresponding bandstructure and run it to obtain the bandstructure diagram, as shown in the figure below. The bandgap range of the photonic crystal is shown as the shaded area in the figure.

Recommend

Photonic Crystal Optical Switch Using Line Defects

The self-collimation(SC) effect of photonic crystals(PCs) achieves collimated radiation with almost no diffraction effect when the incident light propagates along a particular direction of the crystal. Line defects in 2D PCs cause bending and splitting of the SC beam. In this example, the effect of "optical switching" can be achieved by altering the line defects (radius of the dielectric rod) in the photonic crystal.

Bandstructure of 2D Square Lattice

Photonic crystals, as a dielectric structure with periodic changes in dielectric constant, can prevent light of a specific frequency from propagating internally, forming a photonic band gap.

Bandstructure of 2D Triangular Lattice

In this case, a 2D triangular-lattice PC formed by air cylinders arranged in parallel in the medium is constructed, and its bandstructure is calculated.

Bandstructure of BCC Lattice and FCC Lattice

In this case, BCC and FCC photonic crystals are constructed and their bandstructures are analyzed using FDTD solvers.

Bandstructure of a Magneto-Optical Waveguide

In this case, the optical waveguide model with periodic structure in the propagation axis is constructed, and the bandstructure of the waveguide is analyzed.

Correcting Field Amplitudes for High-Q Cavities

Generally, in the simulation of high-Q resonant cavities, the field amplitude obtained is inaccurate. The reason is that the loss rate in the high-Q resonant cavity is slow. If the simulation time is not long enough, the field in the cavity will not decay to 0 at the end of the simulation. At this time, the amplitude of the mode field in the cavity needs to be corrected to obtain the final actual amplitude. This case constructs a photonic crystal resonant cavity structure to demonstrate how to correct the field amplitude when the simulation time of a high-Q resonant cavity is insufficient.

2D-Periodic Metallic Photonic Crystal Slabs

The ability to modify an object's thermal radiation profile is important in many areas of applied physics and engineering. It has been noted that periodic engineering of devices made of metallic and dielectric materials at the subwavelength scale can change the thermal radiation properties of the device. This case studies the thermal radiation of a photonic crystal obtained by periodically arranging a device made of metallic tungsten and a dielectric material.

Organic Solar Cell with PC Structure

How to improve Organic solar cells'(OSCs) photoelectric conversion efficiency (PCE) is an urgent problem to be solved. One of the more commonly used methods is to add micro-nano structures for light trapping into the photoactive layer of OSCs to increase light absorption, thereby improving PCE. The photonic crystal (PC) structure is used in the photoactive layer of OSCs, which can enhance the light absorption of solar cells in specific wavelength bands. This case uses FDTD simulation to analyze the light absorption of an OSC with a 2D hexagonal-lattice PC structure.

Exciting the Surface Plasmon-Polaritons in Graphene

The chemical potential of graphene can be regulated by methods such as voltage or chemical doping. This property makes graphene highly versatile in the field of material-light interactions, particularly in relation to surface plasmon polaritons (SPPs). By exciting surface plasmons, graphene significantly enhances its ability to interact with light.

Bandstructure of Woodpile Lattice

In this case, the Woodpile-Lattice photonic crystal is constructed, and the FDTD solver is used to explore the energy bandstructure of the photonic crystal.