Preface

A black body is an idealized object that can absorb all external electromagnetic radiation without any reflection or transmission. As the temperature rises, the electromagnetic waves radiated by the black body are called black body radiation. Actual objects cannot completely absorb external electromagnetic radiation, so they are also called "gray bodies". The thermal radiation spectrum of a "gray body" can be altered by changing its geometry or the materials used. The ability to modify or tailor the thermal radiation profile of an object is of great importance in many areas of applied physics and engineering. It has been noted that periodic engineering of devices made of metallic and dielectric materials at the subwavelength scale can change the thermal radiation properties of the device. Based on the work of Chan^[1] et al., this case studies the thermal radiation of a photonic crystal obtained by periodically arranging a device made of metallic tungsten and a dielectric material with a refractive index of $\sqrt{5}$.

Simulation Setting

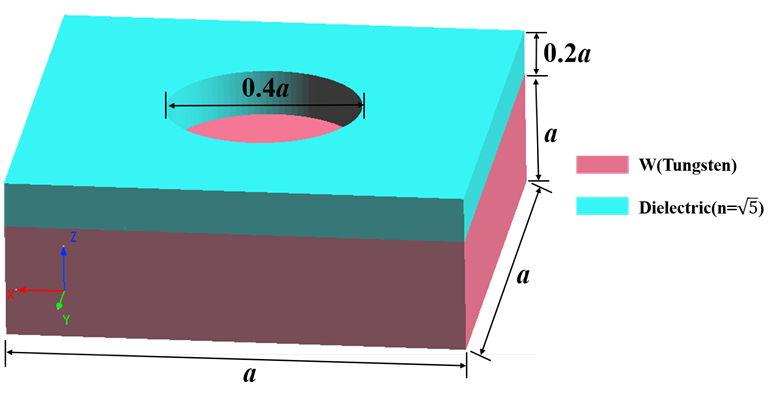
The photonic crystal used in this case is made of a dielectric material with a periodic hole array placed on a metal tungsten slab. The following figure is a schematic structural diagram of a cell of the crystal, where $a$ is the lattice constant of the photonic crystal. Due to the symmetry of the structure and plane wave source, we use Anti-Symmetric boundary conditions in the $X$ direction and Symmetric boundary conditions in the $Y$ direction. You can use symmetric and anti-symmetric boundary conditions to reduce the simulation region to 1/4, thereby reducing the memory and time used by the simulation.

Material

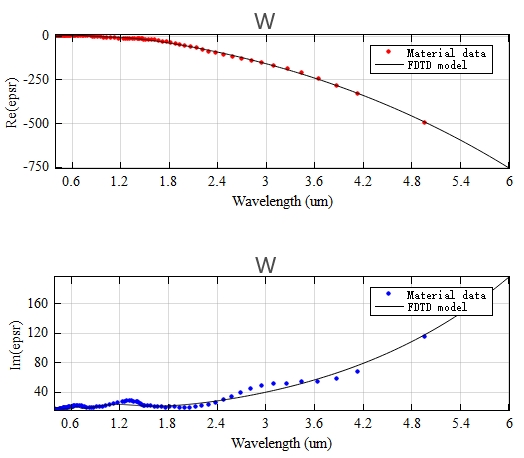
In this case, the permittivity of tungsten metal will affect the performance of the device. Therefore, before simulating, it is necessary to check whether the fitted model within the simulation band meets the simulation requirements. If it does not, adjust the fitting error and the max coefficient of a polynomial and refit a model. The figure below shows the results of automatic fitting in this case that meet the error requirements.

Simulation Results

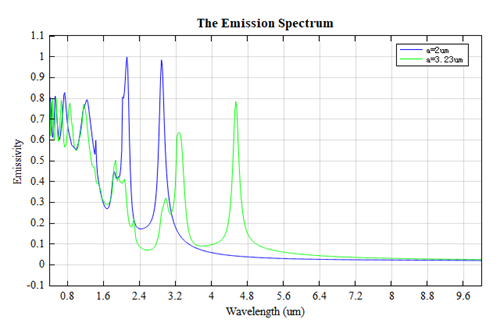
Through the T data stored in the Frequency-Domain Field and Power(FDFP) monitors at the top and bottom of the structure, the reflectivity, transmissivity and absorptivity (i.e. emissivity) of the device can be plotted. The distribution of emissivity with wavelength when the photonic crystal lattice constant $a$ is $2\mu m$ and $3.23 \mu m$, respectively, is shown in the figure below.

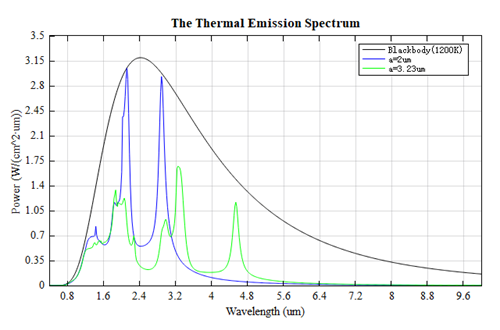
The thermal radiation spectra can be obtained by multiplying the emissivity by the blackbody radiativity. They are shown in the figure below together with the blackbody radiation spectrum, consistent with Figure5(b) in the reference. Detailed information about the thermal radiation calculation in this case can be found in the thermal_emission_power analysis group in the attached project. See the appendix for relevant information about thermal radiation.

Appendixes

Black-body radiation law

The black body radiation law (also known as Planck's black body radiation law, Planck's law) reveals the relationship between the spectral radiant exitance $E_{\lambda}$ of a black body and the wavelength $\lambda$ and temperature $T$. According to the theory of quantum mechanics, Planck's law has the following mathematical expression:

$E_{\lambda}=\frac{c_1\lambda^{-5}}{e^{c_2/\lambda T}-1}$

where $T$ is the absolute temperature (unit $K$), $c_1$ is the first radiation constant, $c_2$ is the second radiation constant, where $c_1= 3.742 \times 10^{-16} (W•m^2)$，$c_2= 1.4388 \times 10^{-2} (m•K)$. Later, Planck proposed the hypothesis of energy discontinuity (a system composed of resonators with a limited number of characteristic frequencies). The total energy of the system is distributed as an integer multiple of the minimum energy unit, which is $hν$, and $h$ is Planck constant ($h \approx 6.626 \times 10^{-34}J•s$), then the discontinuous Planck radiation law can be obtained:

$E_{\lambda}=\frac{2 \pi hc^2\lambda^{-5}}{e^{hc/k_B\lambda T}-1}$

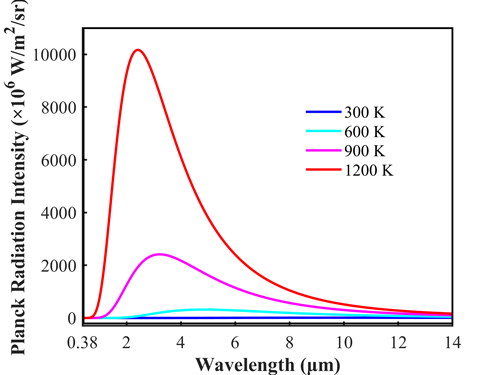
Wherein, $k_B$ is Boltzmann constant ($k_B\approx 1.381×10^{-23}J•K^{-1}$). The thermal radiation spectra of a black body at different temperatures are shown in the figure below. It can be seen from the figure that the thermal radiation of a black body is related to temperature. As the temperature increases, the radiation intensity increases and the radiation peak is blue-shifted.

References