粒子群优化算法

本节是关于粒子群优化算法的介绍。

粒子群优化算法（Particle Swarm Optimization, PSO）最初用于模拟鸟群或鱼群的社会行为，是一种基于群体协作的随机优化技术，现已被广泛应用于包括纳米光子设计在内的各种优化问题中^[1]^[2]。粒子群优化算法的核心是通过群体中个体之间的协作和信息共享来寻找最优解。

粒子群优化算法的基本原理

在粒子群算法寻求最优解的过程中，每个粒子都存在个体行为和群体行为，每个粒子都会学习同伴的飞行经验和借鉴自己的飞行经验去寻求最优解。每个粒子都会向两个值学习，一个值是个体的历史最优值 $p_{best}$ ；另一个值是群体的全局最优值 $g_{best}$ 。粒子会根据这两个值来调整自身的速度和位置，而每个位置的优劣都是根据适应度值来确定的。适应度函数是优化的目标函数。

粒子和速度初始化

在一个 $D$ 维的目标搜索空间中，有 $N$ 个粒子组成一个粒子群，其中每个粒子都是一个 $D$ 维向量，其空间位置可以表示为：

$x_i=(x_{i1},x_{i2},... ,x_{iD}),i=1,2,3,...,N$

粒子群的空间位置是目标优化问题中的一个解，将其代入适应度函数可以计算出适应度值，根据适应度值的大小衡量粒子的优劣。
第 $i$ 个粒子的飞行速度也是一个 $D$ 维向量，记为：

$v_i=(v_{i1},v_{i2},... ,v_{iD}),i=1,2,3,...,N$

粒子的位置和速度的均值都在给定的范围内随机生成。

个体历史最优值和全局最优值

第i个粒子经历过的具有最优适应度值的位置称为个体历史最优位置，记为：

$p_{besti}=(p_{besti1},p_{besti2},... ,p_{bestiD}),i=1,2,3,...,N$

整个粒子群经历过的最优位置称为全局历史最优位置，记为：

$g_{besti}=(g_{besti1},g_{besti2},... ,g_{bestiD}),i=1,2,3,...,N$

粒子群的速度和位置更新

粒子群的位置更新操作可用速度更新公式和位置更新公式表示。
速度更新公式为：

$v_{ij}(t+1)=v_{ij}(t)+c_1r_1(p_{bestij}(t)-x_{ij}(t))+c_2r_2(g_{bestj}(t)-x_{ij}(t))$

位置更新公式为：

$x_{ij}(t+1)=x_{ij}(t)+v_{ij}(t+1)$

其中，下标 $j$ 表示粒子的第 $j$ 维，下标 $i$ 表示第 $i$ 个粒子， $t$ 表示当前迭代次数， $c_1$ 与 $c_2$ 为加速常量，通常在区间 $(0,2)$ 内取值， $r_1$ 与 $r_2$ 为两个相互独立的随机数，在区间 $[0,1]$ 内取值。从上述方程可以看出， $c_1$ 与 $c_2$ 将粒子向个体学习和向群体学习联合起来，使得粒子能够借鉴自身的和群体的搜索经验。

粒子群优化算法流程

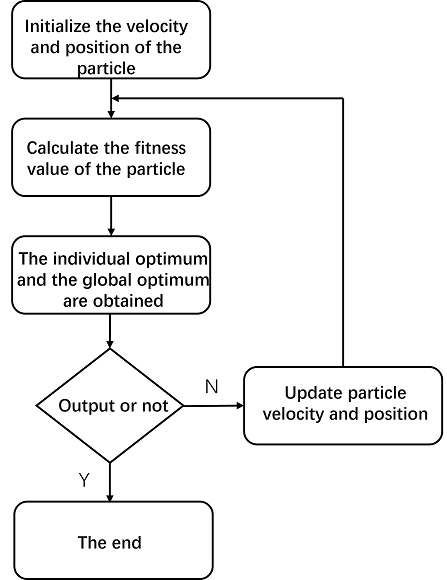
粒子群优化算法的流程如下：

初始化粒子群参数 $c_1$ 和 $c_2$ ，设置位置边界范围和速度边界范围，初始化粒子群的速度和位置；
根据目标函数计算目标值，记录历史最优值 $p_{best}$ 和全局最优值 $g_{best}$ ；
利用速度更新公式对粒子群的速度进行更新，并对越界的速度进行约束；
利用位置更新公式对粒子群的位置进行更新，并对越界的位置进行约束；
根据目标函数计算新的目标值；
将每个粒子的新目标值与它的历史最优目标值相比较，若更好，则将其更新为新的历史最优值 $p_{best}$ ；
将每个粒子的新目标值与群体所经历的最优目标值相比较，若更好，则将其更新为新的全局最优值 $g_{best}$ ；
判断是否达到结束条件（达到最大迭代次数），若达到，则输出最优位置，否则重复步骤3-8。

参考文献

Robinson J , Rahmat-Samii Y .Particle Swarm Optimization in Electromagnetics. IEEE Trans. on Antennas and Propagation 52(2), 397-407[J].IEEE Transactions on Antennas and Propagation, 2004, 52(2):397-407. ↩︎
Parsopoulos K E , Vrahatis M N .Particle Swarm Optimization and Intelligence (Advances and Applications) || Applications in Bioinformatics and Medical Informatics[J]. 2010, 10.4018/978-1-61520-666-7(chapter 9):204-221. ↩︎