FDFP监视器的设置

本节是关于频域场功率（Frequency domain field and power, FDFP）监视器设置的介绍。

FDFP监视器用于计算指定几何空间中的频域电磁场的数据。

在求解器选项卡中选择FDFP monitor，在复合视图中单击，并在自动弹出的属性编辑界面设置相关参数，以完成FDFP监视器的创建。

FDFP监视器计算处理

时域、空域、频域定义的物理量由傅里叶变换联系在一起，而FDFP监视器可以将时域场信号转换为频域场信号。因此，FDFP监视器不仅能够记录数据，还能够计算处理数据。

电场和磁场

电场

FDFP监视器返回的频域电场公式如下：

$\boldsymbol{E}(\omega) = \int \boldsymbol{E}(t) e^{-i\omega t}dt$

$\boldsymbol{E}(t)$为时域电场，$e^{-i\omega t}$为复指数函数，$t$为时间。

磁场

FDFP监视器返回的频域磁场公式如下：

$\boldsymbol{H}(\omega) = \int \boldsymbol{H}(t) e^{-i\omega t}dt$

$\boldsymbol{H}(t)$为时域磁场，$e^{-i\omega t}$为复指数函数，$t$为时间。

能量、功率、透过率

坡印廷矢量

FDFP监视器的坡印廷矢量计算公式如下：

$\boldsymbol{P}(\omega) = \boldsymbol{E}(\omega)\times \boldsymbol{H}(\omega)^*$

$\boldsymbol{E}(\omega)$为频域电场，$~\boldsymbol{H}(\omega)^*~$为频域磁场的共轭复数。

功率

FDFP监视器的功率计算公式如下：

$power = \int \boldsymbol{P}(\omega) \cdot d\boldsymbol{s}$

$\boldsymbol{P}(\omega)$为坡印廷矢量，$d\boldsymbol{s}$为表面法向。

透射率

FDFP监视器的透射率计算公式如下：

$T(\omega) = \frac{0.5\int Re(\boldsymbol{P}(\omega))\cdot d\boldsymbol{s}}{source power(\omega)}$

$\boldsymbol{P}(\omega)$为坡印廷矢量，$source power(\omega)$为入射功率，$d\boldsymbol{s}$为表面法向。

FDFP监视器的设置

通用设置

General标签页是关于FDFP监视器的通用设置。

数据监测

Name	Description
Data type	记录数据的数据类型，默认为Frequency-domain，只读参数。
Spatial interpolation	下拉选择空间插值的类型：None：不进行任何空间插值操作，记录网格内不同位置的电磁场分量；Mesh cell：电场和磁场的每个分量被记录在网格的不同位置，当用户选择Mesh cell插值类型后，电磁场的分量就会被插值到最近的网格单元边界上。这种插值方式是将场分量内插到网格的同一位置，以确保坡印廷矢量的正确计算。
Record data in PML	记录PML区域内的数据，此项为高级设置，默认不勾选。

分量

Name	Description
Components	电磁场分量：Ex、Ey、Ez；Hx、Hy、Hz；坡印廷矢量：Px、Py、Pz。

频率采样

Name	Description
Min sampling per cycle	每个周期的最小采样数；用于设置每个周期内采样的点数，默认值为2。
Desired sampling	期望采样；用于控制采样密度的参数，指定仿真过程中对场进行采样的间隔或步长。
Nyquist limit	奈奎斯特采样极限；为了能够准确地重构一个连续时间信号，必须以不低于待分析信号最高频率两倍的采样率对信号进行采样。
Sampling frequency	采样频率；表示单位时间内对连续信号进行采样的次数。采样频率应不低于待分析信号最高频率的两倍，以遵循奈奎斯特极限的要求。
Sample time(per # of dt)	采样时间；在仿真过程中进行采样的时间间隔，即在多少个时间步长之后对场进行一次采样。

空间采样

Name	Description
Per # of dx/dy/dz	仿真过程中沿着X/Y/Z方向采样的间隔，即在多少个离散化步长之后进行一次采样。

几何尺寸

Geometry是FDFP监视器几何尺寸设置标签页。详情请参阅监视器的几何尺寸设置。

波长/频率

频率设置

Frequency settings标签页用于设置FDFP监视器的带宽范围和频点数。

• 基于光源的设置

勾选Base on source setting后，该标签页的波长/频率范围显示光源的波长/频率范围，且波长/频率范围的设置选项卡为只读状态。

取消勾选Base on source setting后，该标签页的波长/频率范围允许自定义。

• 简化编辑

Edit simplified settings为监视器自定义波长范围的简化编辑方式。

• 复杂编辑

Edit complicated settings为监视器自定义波长/频率范围的复杂编辑方式。

切趾

傅里叶变换是研究整个时域和频域的关系。在仿真过程中无法对无限长的信号进行测量和运算，而是取其有限的时间片段进行分析。可采用不同的窗口函数对信号进行切趾，利用窗口函数将采样区域边缘的信号平滑地降至零。

Name	Description
Apodization type	下拉选择切趾类型。
Apodization function	下拉选择切趾窗函数类型。
Apodization center	窗函数中心位置，即时域信号开始衰减的位置。
Apodization time width	控制窗函数在时间域上的宽度，即窗函数从开始生效到完全衰减所经过的时间。较短的时域宽度会导致更快的衰减速度，而较长的时域宽度则会产生更缓慢的衰减。

切趾类型可分为以下三种：

Name	Description
None	不对时域信号切趾。
Full	时域完整的窗口函数，时域信号转换为频率后，仅窗口处数据会保留。
Start	从时域信号的起始位置处进行衰减，过滤前端的时域数据。
End	从时域信号的结束位置处进行衰减，过滤仿真后端的时域数据。

软件内置的窗口函数类型有以下九种，每种窗口函数都有不同的特性，用户可以根据实际需求选择合适的窗函数：

Gaussian：在时域上呈现出高斯分布的形状，具有平滑的衰减特性。高斯窗口函数在频域上的主瓣较宽，因此频率分辨力低。其表达式为：

$\omega(t)={e}^{-\frac{t^2}{2 {\sigma}^2}}$

$\sigma$是控制窗口带宽的标准差参数，$t$是时间。

Bartlett：在时域上呈三角形，具有平滑的衰减特性。它的幅度从窗口中心向两端逐渐减小，类似于一个对称的三角形Bartlett窗函数。在频域上具有较宽的主瓣和相对较高的旁瓣功率，因此在需要较好的频谱分辨率和较小的旁瓣泄漏时，可能需要考虑其他类型的窗口函数，如Hanning窗、Hamming窗、Blackman窗等。其表达式为：

$\omega(t)=1-\frac{|t|}{T}$

$t$是时间，$T$是窗口的时域宽度。

Blackman：在时域上呈平滑的衰减特性，包含了一个主要的余弦项和一个次要的余弦项，这使得它在频域上能够提供更好的旁瓣抑制和频谱分辨率。其表达式为：

$\omega(t) = 0.42 - 0.5 \cos\left(\frac{2\pi t}{T}\right) + 0.08 \cos\left(\frac{4\pi t}{T}\right)$

$t$是时间，$T$是窗口的时域宽度。

Connes：在时域上振幅分布呈平滑的曲线形状。与其他窗口函数相比，它在起始和结束位置处的振幅衰减更加缓慢。其表达式为：

$\omega(t) = \left(1 - \frac{t^2}{(\frac{T}{2})^2}\right)^2$

$t$是时间，$T$是窗口的时域宽度。

Cosine：在时域上振幅分布呈周期性变化，从最小值到最大值，再回到最小值。这种周期性变化使得时域信号的振幅均匀分布。其表达式为：

$\omega(t) = cos\left(\frac{\pi t}{T}\right)$

$t$是时间，$T$是窗口的时域宽度。

Hanning：在时域上呈平滑的衰减特性，类似于余弦波形。Hanning窗口函数的优点是平滑衰减的形状有助于减小频谱泄漏，提供较好的频谱分辨率。缺点是在时域上的平滑衰减特性会导致频域上的主瓣宽度增加。其表达式为：

$\omega(t)=0.5-0.5cos(\frac{2\pi t}{T})$

$t$是时间，$T$是窗口的时域宽度。

Hamming：在时域上呈现出平滑的衰减特性，类似于余弦波形，与Hanning窗函数类似。Hamming窗函数具有较低的旁瓣功率和频谱泄漏。与Hanning窗函数相比，Hamming窗函数在窗口两端的值衰减得更快，因此在频谱分析中能够提供更好的旁瓣抑制能力，但同时也会导致较宽的主瓣。其表达式为：

$\omega(t) =0.54 - 0.46cos(\frac{2\pi t}{T})$

$t$是时间，$T$是窗口的时域宽度。

Welch：在时域上呈类似于抛物线的形状，具有较好的旁瓣抑制能力。它与Bartlett窗函数类似，但在窗口两端的衰减速率更快。其表达式为：

$\omega(t) = 1 - \frac{t^2}{(\frac{T}{2})^2}$

$t$是时间，$T$是窗口的时域宽度。

Uniform：矩形窗口函数；窗口内部取值为常数1，窗口外部取值为0。该函数的优点是主瓣比较集中，缺点是没有平滑衰减特性，具有较大的频谱泄漏和旁瓣功率。其表达式为：

$\omega(t)=\begin{cases} 1 & -\frac{T}{2}\leq t \leq \frac{T}{2} \\ 0 & otherwise \\ \end{cases}$

$t$是时间，$T$是窗口的时域宽度。

模式扩展

Mode expansion为FDFP监视器的模式扩展的设置，具体的设置细节请参阅FDFP监视器模式扩展。

数据可视化

使用FDFP监视器保存由时域仿真计算得到的频域场数据集，返回的结果数据包括：

• E：电场与频率（波长）的关系；
• H：磁场与频率（波长）的关系；
• P：坡印亭矢量与频率（波长）的关系；
• Power：功率与频率（波长）的关系；
• T：透射率与频率（波长）的关系。

在FDFP监视器的可视化窗口中，可查看该频域场分布，操作如下图：

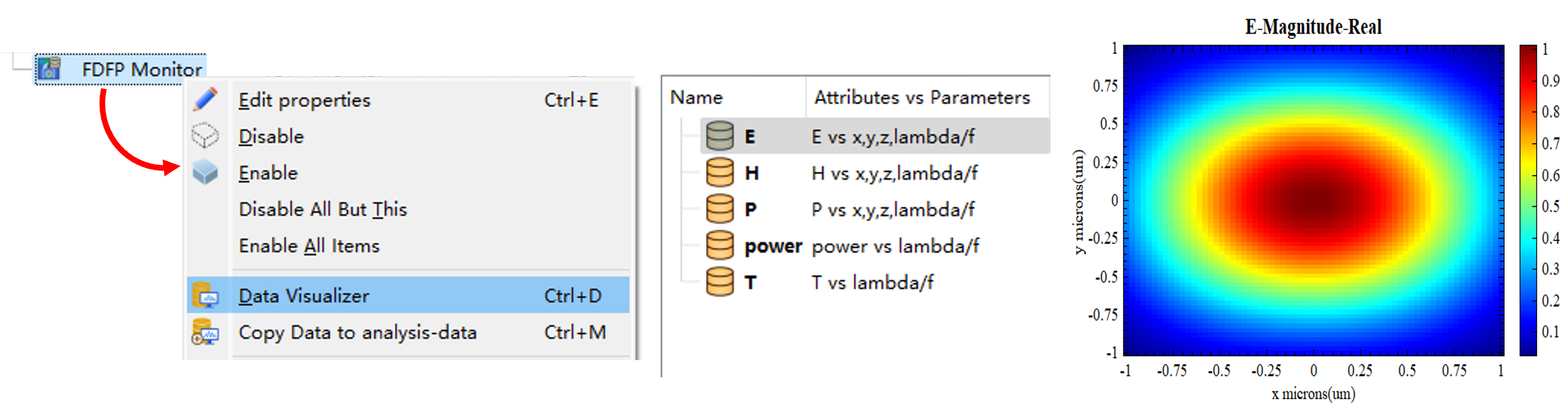
在数据可视化界面，可实现对数据的选取、绘制和保存等操作，详情请参阅数据可视化。

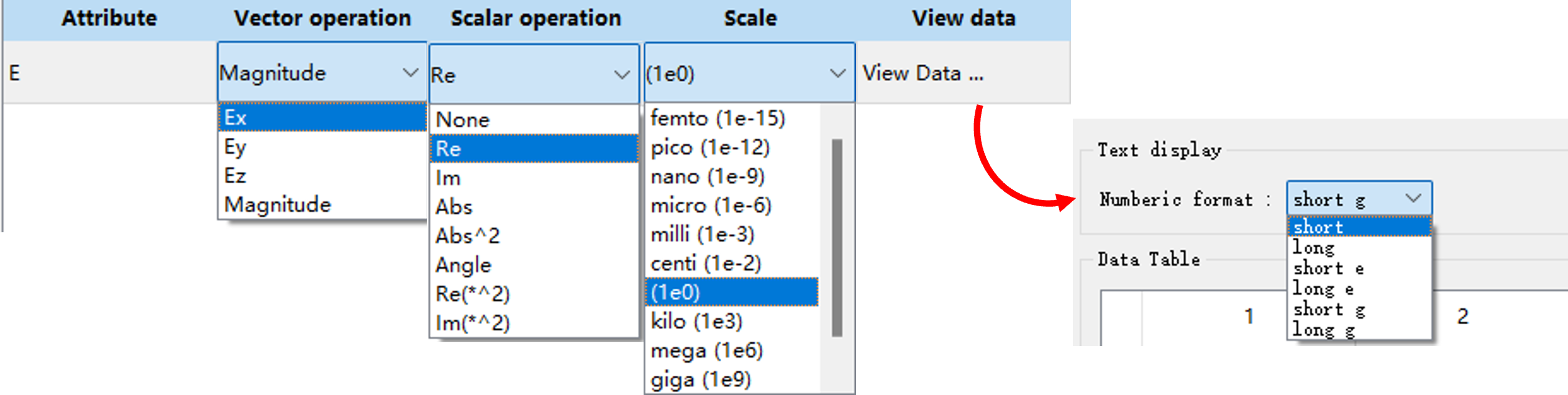
比如查看$E_x$分量的实部，Attributes的设置和结果如图所示：

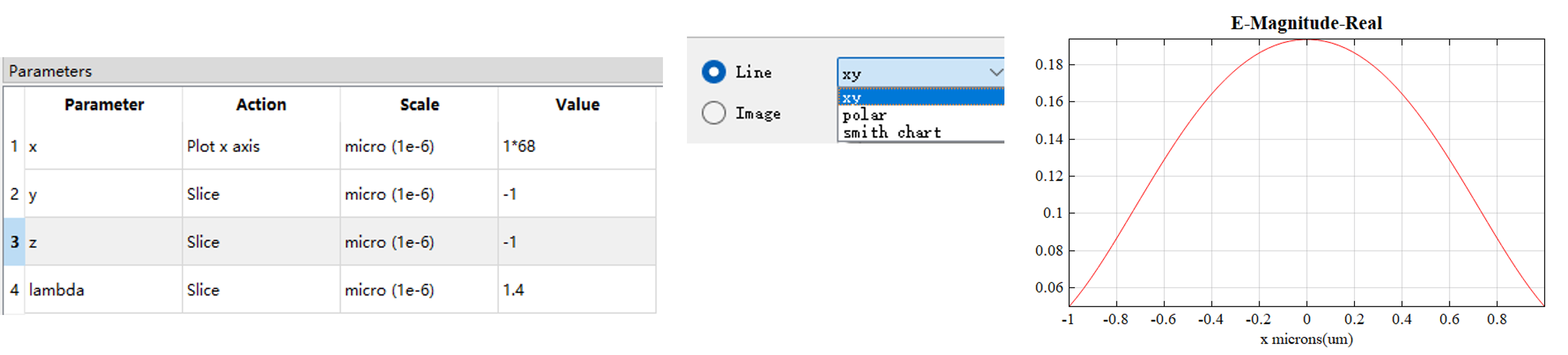
将一维数据集绘制为1D线图：