前言 #

集成光子学已成为光通信、传感和信号处理等领域的重要支撑技术。在众多光子器件中，环形谐振器因其结构紧凑、品质因数高以及优异的波长选择特性，被广泛应用于滤波、调制和非线性光学等场景。为了在目标波长范围内获得理想的谱响应，设计阶段必须进行精确的参数优化与性能预测。本案例设计仿真了一个中心波长为$1.55 \mu m$,自由频谱宽度（Free Spectral Range, FSR）为$3200GHz$的环形谐振器。

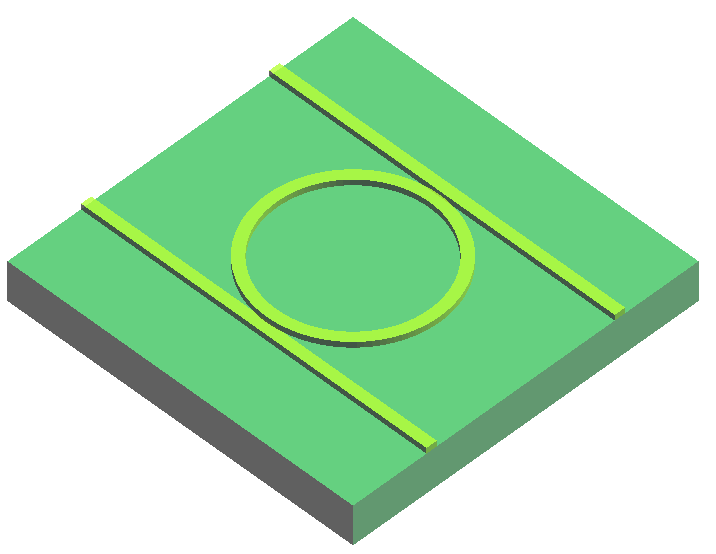
本文将首先利用 FDE 求解器计算$n_{eff}$和$n_g$，并据此选择合适的微环半径。随后，在已确定半径的条件下，分别采用 2.5D 以及3D 的 FDTD 求解器对该谐振器进行仿真，获得从输入端口耦合至$drop$端口的透射谱及$Q$值，并将结果与 3D FDTD 仿真结果进行对比，以验证设计的准确性与仿真方法的可靠性。

仿真设置 #

模型简介 #

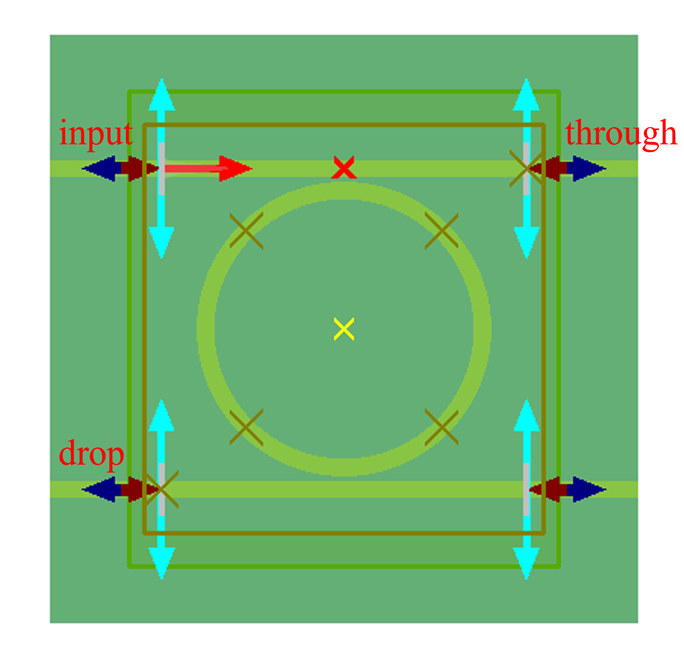
本案例采用的仿真模型如上图，波导结构为$0.4 \mu m \times 0.22 \mu m$的 SOI 波导。双直波导宽度$wg_{width}$与微环波导宽度$ring_{width}$相等，波导间距$gap$设置为$0.1 \mu m$。

设计要求在中心波长$1.55\mu m$处，谐振峰之间的距离（FSR）达到$3200GHz$（对应的波长间隔为$25.6 nm$）。为了满足这一条件，微环半径$R$需要同时满足以下两个公式

$R=\frac{m \lambda}{2\pi n_{eff}},\space R=\frac{\lambda^2}{2\pi n_g FSR}$

其中，$n_{eff}$、$n_g$分别为$1.55\mu m$的波长下的有效折射率与群折射率。第一个公式源于微环谐振的模式条件，保证光场在环内传播一周后相位满足相干条件；第二个公式来源于 FSR 与环长的关系，确保谐振峰间距满足设计要求。

求解器设置 #

由于硅材料在光学波段为色散介质，为保证材料模型在频率范围内的连续性，需要在FDE求解器中将sampled material data sampling type设置为使用多项式材料模型拟合材料数据。

环形谐振器是一种高 Q 值的器件，为了得到更准确的仿真结果，需要较长的仿真时间，本案例中需要将 FDTD 仿真时间设置为 5 ps。在 2.5D FDTD 仿真中，由于入射光源带宽为$0.1\mu m$，且需考虑波导色散，应在2.5D setting选项卡中勾选Broad bandwidth。此外，slab position应当选择波导所在的位置，具体可参考2.5D 求解器中的说明。

仿真结果 #

有效折射率与群折射率 #

打开附件中的 RingResonator_FDE.mpps 工程，运行 neff_ng.msf 脚本可自动设置 FDE 求解器进行模式求解与频率扫描，得到$1.55\mu m$波长下的有效折射率和群折射率：

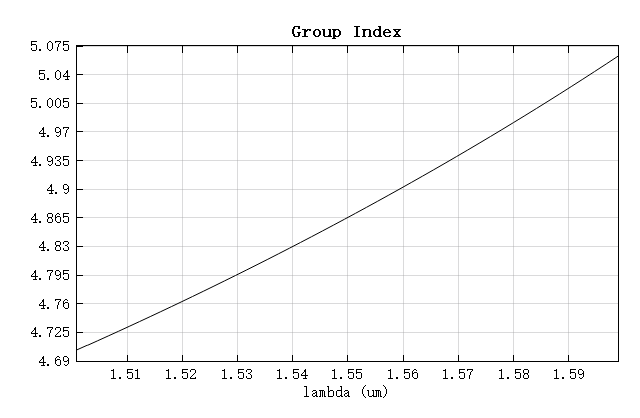
计算结果表明，有效折射率$n_{eff}=2.1155$，群折射率$n_g=4.865$。当$m=27$时，两公式计算的半径最为接近，此时圆环半径约为$3.15 \mu m$

各端口透射谱 #

在 2.5D 和 3D 仿真前，均需要使用 RingResonator_structure.msf 脚本对圆环半径及端口位置等参数进行设置。下面分别给出两种仿真方法下的透射谱结果。

首先，运行 RingResonator_2.5d.mpps 工程，仿真完成后，通过 RingResonator.msf 脚本可在获得四个端口中波长与透射率的关系：

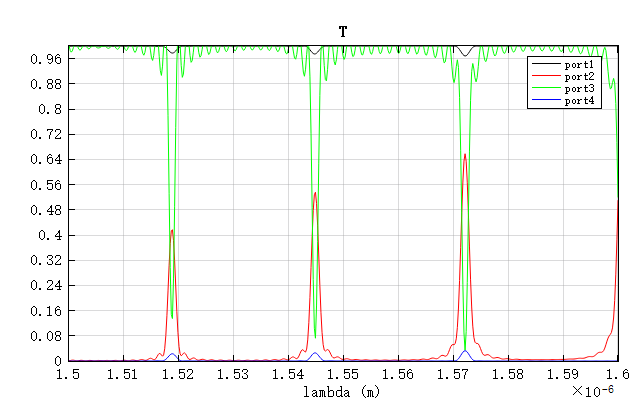
结果显示，存在三个明显的谐振峰，其中中心波长为$1.545\mu m$，与设计值相差不到1%。该结果验证了 2.5D FDTD 在快速建模和分析中的有效性。

随后，运行 RingResonator_3d.mpps 工程，得到的透射谱如下图所示：

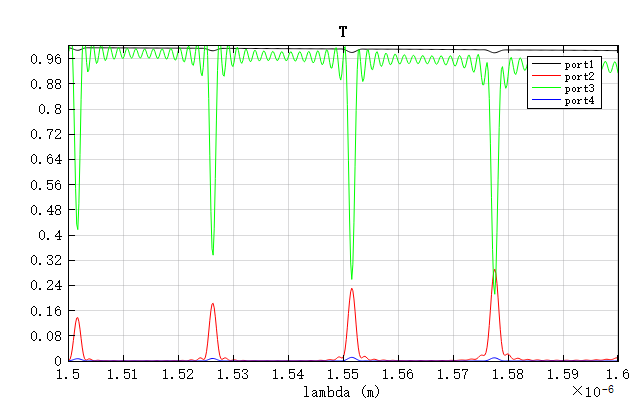
可以看到，3D 仿真得到的中心波长为$1.551 \mu m$，相比 2.5D 仿真结果更接近设计值，说明 3D FDTD 在准确性上具有优势。下文中的结果分析均为3D仿真结果。

共振波长下的电场分布 #

根据输出端口的共振峰，查看 FDFP monitor ZX 的数据。共振峰处的电场强度如下图右所示。很明显，相对于非共振波长$1.54 \mu m$（下图左），场值明显增强。

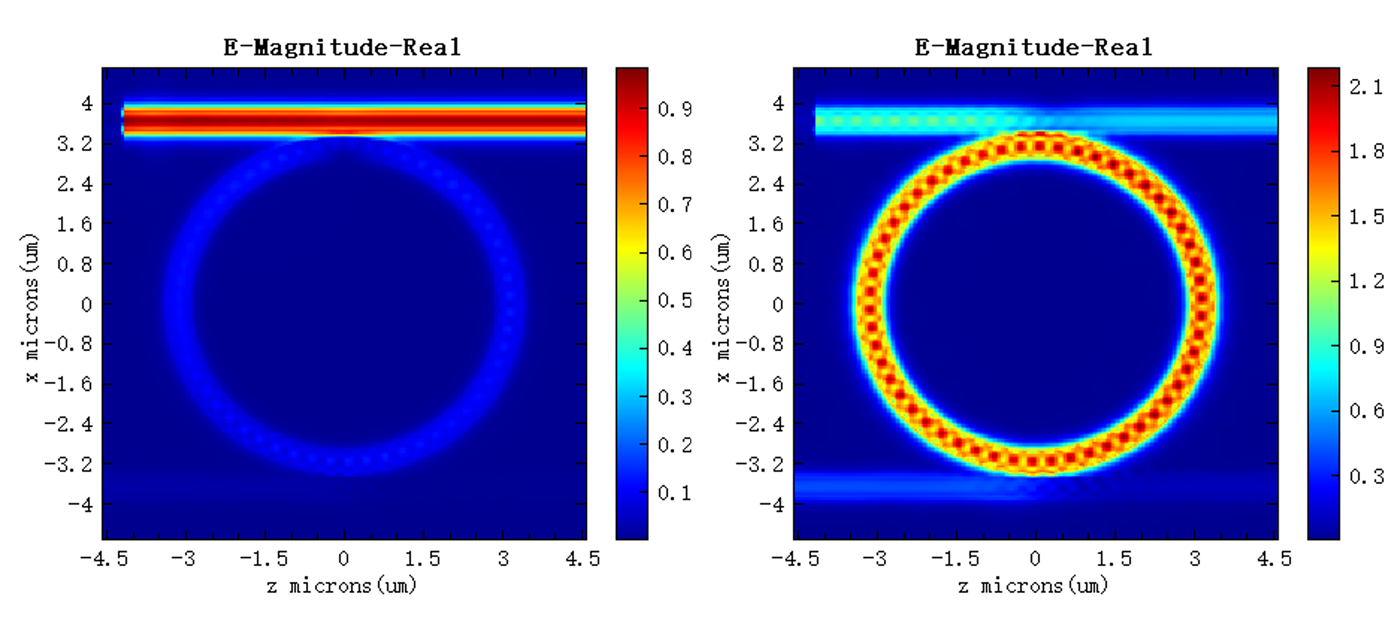
品质因子 #

利用工程中的 High Q analysis分析组，可得到三个谐振峰的品质因子（Q） 值：

[High Q analysis::analysis script result] 
val =
Resonance 1:  
val =
    frequency = 193.219THz, or 1551.57 nm  
val =
    Q = 2471 +/- 0.0192705  
val =
Resonance 2:  
val =
    frequency = 196.43THz, or 1526.21 nm  
val =
    Q = 3257.29 +/- 0.000534521  
val =
Resonance 3:  
val =
    frequency = 190.071THz, or 1577.27 nm  
val =
    Q = 1815.94 +/- 0.127365 

与理论结果对比 #

使用附件中的 RingResonator.msf 脚本计算出中心波长$1.55\mu m$，$FSR=3200GHz$时，$drop$端口的理论频谱并与仿真结果进行对比，如下图所示。

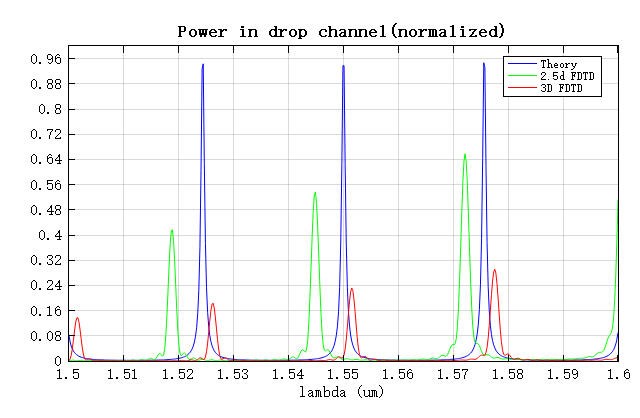
对比结果表明，FSR 与理论值吻合良好；3D FDTD 仿真得到的总透射率较低，主要由于三维仿真中引入了更多损耗因素。共振峰的精确位置对环形谐振器的有效光学长度极为敏感。两种仿真方法使用的结构相同，但在 2.5D 仿真中需要将 3D 材料等效为 2D 材料，这一过程会引入一定的近似误差，导致有效光学长度与 3D 仿真略有差异，因此峰的位置会出现轻微偏移。

参考文献 #

[1] Mirza, Asif , et al. "Silicon Photonic Microring Resonators: Design Optimization Under Fabrication Non-Uniformity." Design, Automation and Test in Europe Conference and Exhibition 2020.
[2] 周治平. 硅基光电子学. 北京大学出版社, 2012.
[3] Hammer, Manfred , K. R. Hiremath , and R. Stoffer . "Analytical Approaches to the Description of Optical Microresonator Devices." Aip Conference Proceedings (2004).